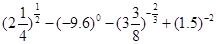题目内容
(本题满分10分) 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=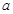 (
(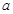 >2),BC=2,且AE=AH=CF=CG,
>2),BC=2,且AE=AH=CF=CG,
设AE= ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于 的函数关系式,并指出这个函数的定义域;
的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积 最大?
最大?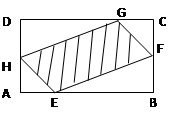
(1)SΔAEH=SΔCFG=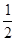 x2, SΔBEF=SΔDGH=
x2, SΔBEF=SΔDGH=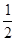 (
(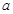 -x)(2-x)
-x)(2-x)
∴y=SABCD-2SΔAEH-2SΔBEF=2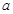 -x2-(
-x2-(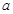 -x)(2-x)=-2x2+(
-x)(2-x)=-2x2+(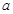 +2)x
+2)x
∴y=-2x2+(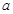 +2)x,0<x≤2
+2)x,0<x≤2
(2)当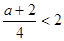 ,即
,即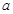 <6时,则x=
<6时,则x= 时,y取最大值
时,y取最大值
当 ≥2,即
≥2,即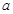 ≥6时,y=-2x2+(
≥6时,y=-2x2+(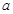 +2)x,在
+2)x,在 0,2]上是增函数,
0,2]上是增函数,
则x=2时,y取最大值2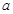 -4
-4
综上所述:当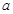 <6时,AE=
<6时,AE= 时,绿地面积取最大值
时,绿地面积取最大值
当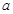 ≥6时,AE=2时,绿地面积取最大值2
≥6时,AE=2时,绿地面积取最大值2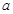 -4
-4
解析

练习册系列答案
相关题目
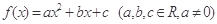 ,
,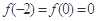 ,
,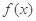 的最小值为
的最小值为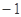 .
.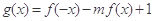 ,若
,若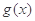 在
在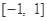 上是减函数,求实数
上是减函数,求实数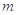 的取值范围;
的取值范围;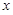 (单位:cm)满足关系:
(单位:cm)满足关系: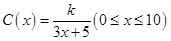 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设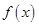 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.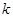 的值及
的值及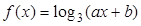 的图象经过点
的图象经过点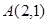 和
和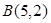 ,记
,记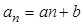 (
( )
)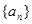 的通项公式;
的通项公式;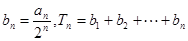 ,若
,若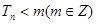 ,求
,求 的最小值;
的最小值;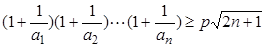 对一切
对一切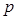 .
.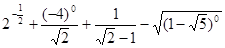
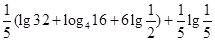
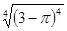 (2)
(2)