题目内容
(本小题13分)已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x.
(1)求f(x)的解析式(2)作出函数f(x)的图象,并指出其单调区间.
(1)当x<0时,-x>0,∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)是定义在R上的偶函数,∴f(-x)=f(x),
∴当x<0时,f(x)=x2+2x.
f(x)=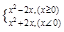
(2)由(1)知作出f(x)的图象如图所示: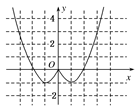
由图得函数f(x)的递减区间是(-∞,-1],[0,1].
f(x)的递增区间是[-1,0],[1,+∞).
解析

练习册系列答案
相关题目
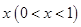 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本)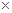 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例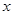 的关系式;
的关系式; 是二次函数,且满足
是二次函数,且满足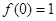 ,
,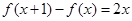
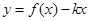 在
在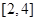 单调,求
单调,求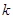 的取值范围。
的取值范围。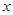 年的年平均污水处理费用
年的年平均污水处理费用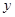 (万元);
(万元);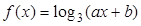 的图象经过点
的图象经过点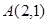 和
和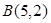 ,记
,记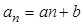 (
( )
)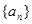 的通项公式;
的通项公式;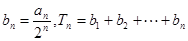 ,若
,若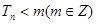 ,求
,求 的最小值;
的最小值;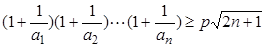 对一切
对一切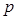 .
.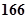 千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于
千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于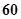 千米/时且不高于
千米/时且不高于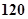 千米/时的时速匀速行驶到杭州.已知该汽车每小时的运输成本
千米/时的时速匀速行驶到杭州.已知该汽车每小时的运输成本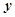 (以元为单位)由可变部分和固定部分组成:可变部分与速度
(以元为单位)由可变部分和固定部分组成:可变部分与速度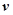 (千米/时)的平方成正比,比例系数为
(千米/时)的平方成正比,比例系数为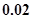 ;固定部分为200元.
;固定部分为200元.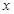 件,服装的实际出厂单价为
件,服装的实际出厂单价为 元,写出函数
元,写出函数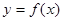 的表达式;
的表达式;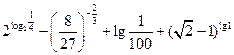
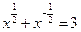 ,求
,求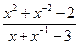 的值.
的值.