题目内容
已知数列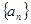 满足
满足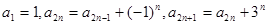 (
( ).
).
(1)求 的值;
的值;
(2)求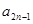 (用含
(用含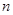 的式子表示);
的式子表示);
(3)记 ,数列
,数列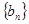
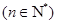 的前
的前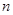 项和为
项和为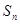 ,求
,求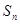 (用含
(用含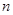 的式子表示).).
的式子表示).).
(1)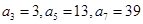 ;(2)
;(2)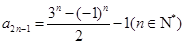 ;(3)
;(3)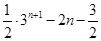 .
.
解析试题分析:(1)求数列的某些项,根据题中条件,我们可依次求得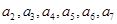 ;(2)从(1)中特殊值可能看不到数列
;(2)从(1)中特殊值可能看不到数列 的项有什么规律,但题中要求
的项有什么规律,但题中要求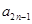 ,那我们看看能否找到此数列的项之间有什么递推关系呢?把已知条件
,那我们看看能否找到此数列的项之间有什么递推关系呢?把已知条件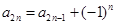 ,代入
,代入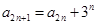 即得
即得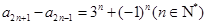 ,由这个递推关系可采取累加的方法求得
,由这个递推关系可采取累加的方法求得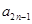 ;(3)首先要求出数列
;(3)首先要求出数列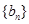 的通项公式
的通项公式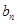 ,由(2)易得
,由(2)易得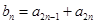
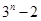 ,从通项公式形式可算出,求其前
,从通项公式形式可算出,求其前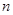 项和可用分组求和法,把它变成一个等比数列的和与一个等差数列的和.
项和可用分组求和法,把它变成一个等比数列的和与一个等差数列的和.
试题解析:(1)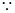
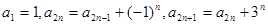 (
( ),
),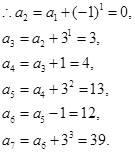
(2)由题知,有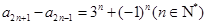 .
.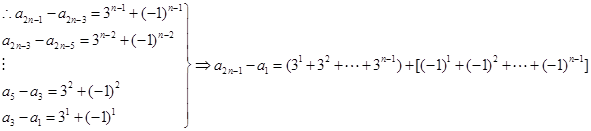 .
.
∴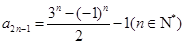 .
.
(3)由(2)可知,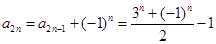 ,
, .
.
∴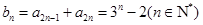 .
.
∴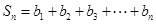
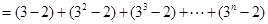
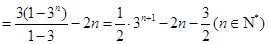 .
.
考点:(1)数列的项;(2)数列的通项公式;(3)分组求和.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 中,
中,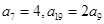 .
.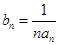 ,求数列
,求数列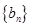 的前
的前 项和
项和 .
.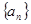 是等差数列,且
是等差数列,且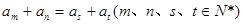 ,
,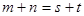 ;
;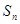 是等差数列
是等差数列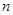 项的和,则
项的和,则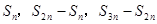 成等差数列;
成等差数列;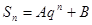 ;(其中
;(其中 是非零常数,
是非零常数,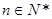 ),则
),则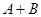 为零.
为零.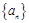 中,
中,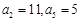 .
. ;
;  项和
项和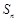 的最大值.
的最大值.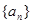 满足
满足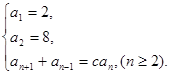 (
(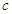 为常数,
为常数,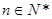 )
)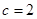 时,求
时,求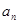 ;
;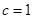 时,求
时,求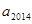 的值;
的值;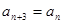 恒成立的常数
恒成立的常数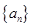 的首项
的首项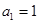 ,公差
,公差 ,且
,且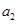 、
、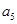 、
、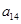 分别是等比数列
分别是等比数列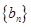 的
的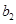 、
、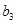 、
、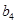 .
.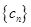 对任意正整数
对任意正整数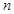 均有
均有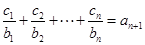 成立,求
成立,求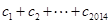 的值.
的值.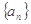 ,等比数列
,等比数列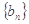 ,满足
,满足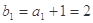 ,
,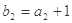 ,
,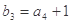 .
.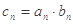 ,求数列{
,求数列{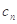 }的前n项和.
}的前n项和.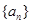 的各项均为正数,
的各项均为正数,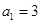 ,前项和为
,前项和为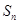 ,
,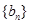 为等比数列,
为等比数列, 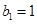 ,且
,且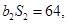
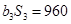 . (1)求
. (1)求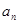 与
与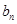 ;
; 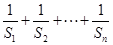 .
.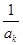 ,
,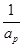 ,
,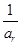 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.