题目内容
设数列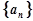 的前n项和为
的前n项和为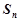 ,
,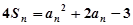 ,且
,且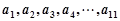 成等比数列,当
成等比数列,当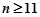 时,
时,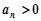 .
.
(1)求证:当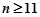 时,
时,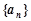 成等差数列;
成等差数列;
(2)求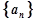 的前n项和
的前n项和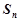 .
.
(1)证明过程详见解析;(2) 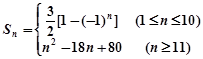
解析试题分析:
(1)利用 和
和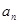 之间的关系(
之间的关系(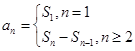 ),可以得到关于
),可以得到关于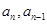 的关系式,再利用十字相乘法可以求的
的关系式,再利用十字相乘法可以求的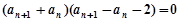 ,再根据题意当
,再根据题意当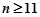 时,
时,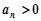 ,则有式子
,则有式子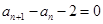 成立,即
成立,即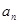 成等差数列.
成等差数列.
(2)利用第(1)问的结果可以得到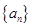 的通项公式,即前11项成等比数列,从11项开始成等差数列,即为一个分段
的通项公式,即前11项成等比数列,从11项开始成等差数列,即为一个分段 ,则其前n项和
,则其前n项和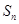 也要分段讨论,即分为
也要分段讨论,即分为 与
与 进行求解.利用等差与等比数列前n项和公式即可得到相应的
进行求解.利用等差与等比数列前n项和公式即可得到相应的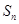 .
.
试题解析:
(1) 由 ,
,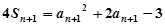 ,
,
得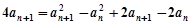 ,
,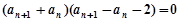 4分
4分
当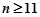 时,
时,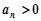 ,所以
,所以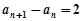 ,
,
所以当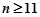 时,
时,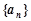 成等差数列. 7分
成等差数列. 7分
(Ⅱ)由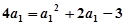 ,得
,得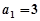 或
或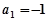
又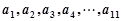 成等比数列,所以
成等比数列,所以 (
(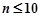 ),
),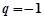 ,
,
而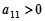 ,所以
,所以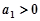 ,从而
,从而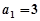 .
.
所以 , 11分
, 11分
所以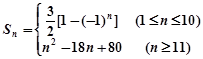 . 14分
. 14分
考点:等差等比数列前n项和 十字相乘法

练习册系列答案
相关题目
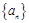 中,
中,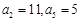 .
.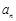 ;
; 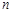 项和
项和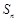 的最大值.
的最大值.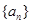 的各项均为正数,
的各项均为正数,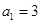 ,前项和为
,前项和为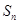 ,
,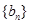 为等比数列,
为等比数列, 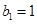 ,且
,且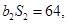
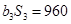 . (1)求
. (1)求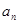 与
与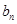 ;
; 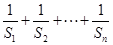 .
.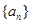 是公差不为0的等差数列,
是公差不为0的等差数列,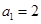 ,且
,且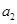 ,
,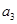 ,
,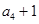 成等比数列.
成等比数列.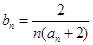 ,求数列
,求数列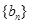 的前
的前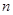 项和
项和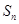 。
。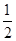 ,an,Sn成等差数列.
,an,Sn成等差数列.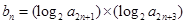 ,求证:
,求证: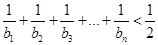 .
.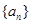 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。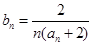 ,求数列
,求数列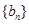 的前
的前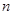 项和
项和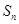
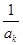 ,
,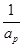 ,
,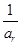 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由. 是等差数列,首项
是等差数列,首项 ,前
,前 项和为
项和为 .令
.令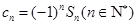 ,
, 的前
的前 项和
项和 .数列
.数列 是公比为
是公比为 的等比数列,前
的等比数列,前 ,且
,且 ,
, .
. 的通项公式;
的通项公式;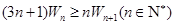 .
.