题目内容
【题目】如图,四楼锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形.
为梯形. ![]() ,且
,且![]() 与
与![]() 均为正三角形.
均为正三角形. ![]() 为
为![]() 的中点
的中点![]() 为
为![]() 重心,
重心, ![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)第(1)问,连![]() 交
交![]() 于
于![]() ,连接
,连接![]() .证明
.证明![]() //
// ![]() ,即证
,即证![]() 平面
平面![]() . (2)第(2)问,主要是利用体积变换,
. (2)第(2)问,主要是利用体积变换, ![]() ,求得三棱锥
,求得三棱锥![]() 的体积.
的体积.
试题解析:
(1)方法一:连![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
由梯形![]() ,
, ![]() 且
且![]() ,知
,知![]()
又![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的重心,∴
的重心,∴![]()
在![]() 中,
中, ![]() ,故
,故![]() //
// ![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]()
![]() 平面
平面![]() .
.
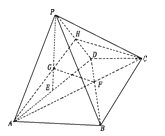
方法二:过![]() 作
作![]() 交PD于N,过F作FM||AD交CD于M,连接MN,
交PD于N,过F作FM||AD交CD于M,连接MN,
![]() G为△PAD的重心,
G为△PAD的重心, ![]()
又ABCD为梯形,AB||CD, ![]()
![]()
又由所作GN||AD,FM||AD,得![]() //
// ![]() ,所以GNMF为平行四边形.
,所以GNMF为平行四边形.
因为GF||MN, ![]()
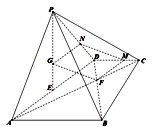
(2) 方法一:由平面![]() 平面
平面![]() ,
, ![]() 与
与![]() 均为正三角形,
均为正三角形, ![]() 为
为![]() 的中点
的中点
∴![]() ,
, ![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由(1)知![]() //平面
//平面![]() ,∴
,∴![]()
又由梯形ABCD,AB||CD,且![]() ,知
,知![]()
又![]() 为正三角形,得
为正三角形,得![]() ,∴
,∴![]() ,
,
得![]()
∴三棱锥![]() 的体积为
的体积为![]() .
.
方法二: 由平面![]() 平面
平面![]() ,
, ![]() 与
与![]() 均为正三角形,
均为正三角形, ![]() 为
为![]() 的中点
的中点
∴![]() ,
, ![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由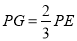 ,∴
,∴![]()
而又![]() 为正三角形,得
为正三角形,得![]() ,得
,得![]() .
.
∴![]() ,
,
∴三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




