题目内容
【题目】(本小题满分16分)设数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 满足:
满足:![]() ,且数列
,且数列![]() 的前
的前
n项和为![]() .
.
(1) 求![]() 的值;
的值;
(2) 求证:数列![]() 是等比数列;
是等比数列;
(3) 抽去数列![]() 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列![]() ,若
,若![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:![]() .
.
【答案】解:(1)由题意得:![]() ;………………1分
;………………1分
当n=1时,则有:![]() 解得:
解得:![]() ;
;
当n=2时,则有:![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
![]()
![]() ………………2分
………………2分
(2)由![]() ①得:
①得:
![]() ② ………………3分
② ………………3分
② - ①得:![]() ,
,
即:![]() 即:
即:![]() ; ……………5分
; ……………5分
![]()
![]() ,由
,由![]() 知:
知:
数列![]() 是以4为首项,2为公比的等比数列.…………………………………8分
是以4为首项,2为公比的等比数列.…………………………………8分
(3)由(2)知:![]() ,即
,即![]() ……………………9分
……………………9分
当n≥2时,![]() 对n=1也成立,
对n=1也成立,
即![]() (n
(n![]() ………………………………………………………….…10分
………………………………………………………….…10分
![]() 数列
数列![]() 为
为![]() ,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………11分
,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………11分
![]() 当n="2k-1"
当n="2k-1"![]() 时,
时,
![]()
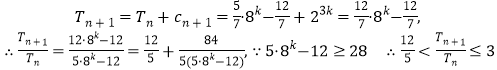 …………………14分
…………………14分
![]() 当n="2k"
当n="2k"![]() 时,
时,
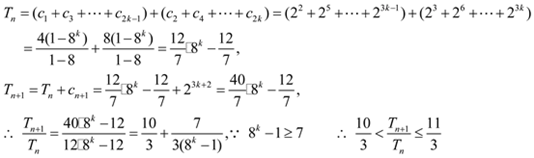
![]()
![]() .……………………………………………………………16分
.……………………………………………………………16分
【解析】
(1)给n取值求出![]() 的值.(2)由题得
的值.(2)由题得![]() 数列
数列![]() 是等比数列.(3)证明当n=2k-1
是等比数列.(3)证明当n=2k-1 ![]() 时,
时,![]() . 当n=2k
. 当n=2k ![]() 时,
时,![]() ,综合即得
,综合即得![]() .
.
(1)由题意得: ![]() ;
;
当n=1时,则有: ![]() 解得:
解得: ![]() ;
;
当n=2时,则有: ![]() ,即
,即![]() ,解得:
,解得: ![]() ;
;
![]() 。
。
(2) 由![]() ① 得:
① 得:
![]() ②
②
② - ①得: ![]() ,
,
即: ![]() 即:
即:![]() ;
;
![]() ,由
,由![]() 知:
知:
数列![]() 是以4为首项,2为公比的等比数列.
是以4为首项,2为公比的等比数列.
(3)由(2)知: ![]() ,即
,即![]() ,
,
当n≥2时, ![]() 对n=1也成立,
对n=1也成立,
即![]() (n
(n![]() ,
,
∴数列![]() 为
为![]() ,它的奇数项组成以4为首项、公比为8的等比数列;
,它的奇数项组成以4为首项、公比为8的等比数列;
偶数项组成以8为首项、公比为8的等比数列;
∴当n=2k-1 ![]() 时,
时,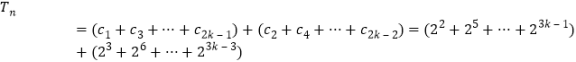
![]()
![]()
![]() ,
,
∴当n=2k ![]() 时,
时,
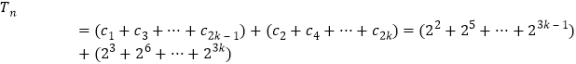
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.

练习册系列答案
相关题目