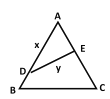
题目内容
【题目】数列![]() 中,
中,![]() ,且对任意的
,且对任意的![]() 成等比数列,其公比为
成等比数列,其公比为![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若对任意的![]() 成等差数列,其公差为
成等差数列,其公差为![]() .设
.设![]() .
.
①求证:![]() 成等差数列并指出其公差;
成等差数列并指出其公差;
②若![]() ,试求数列
,试求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)①证明见解析,
;(2)①证明见解析,![]() ;②
;②![]() 或
或![]() .
.
【解析】
试题分析:(1)公比为![]() ,故
,故![]() 是首相为
是首相为![]() ,公比为
,公比为![]() 的等比数列,,利用前
的等比数列,,利用前![]() 项和公式求得前
项和公式求得前![]() 项和为
项和为![]() ;(2)①根据等差中项,可有
;(2)①根据等差中项,可有![]() ,利用取倒数的方法,配凑成等差数列,即
,利用取倒数的方法,配凑成等差数列,即![]() ,所以
,所以![]() 为等差数列;②由
为等差数列;②由![]() , 解得
, 解得![]() 或
或![]() ,分成两种情况,利用累乘法求得
,分成两种情况,利用累乘法求得![]() 或
或![]() .
.
试题解析:
(1)因为![]() ,所以
,所以![]() ,故
,故![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以
的等比数列,所以 ![]() .
.
(2)①因为![]() 成等差数列, 所以
成等差数列, 所以![]() ,而
,而![]() ,则
,则![]() , 得
, 得![]() , 所以
, 所以![]() , 即
, 即![]() , 所以
, 所以![]() 是等差数列; 且公差为
是等差数列; 且公差为![]() 是等差数列,且公差为
是等差数列,且公差为![]() .
.
②因为![]() ,所以
,所以![]() ,则由
,则由![]() , 解得
, 解得![]() 或
或![]() .(i)当
.(i)当![]() 时,
时,![]() , 所以
, 所以![]() ,则
,则![]() ,即
,即![]() ,得
,得![]() , 所以
, 所以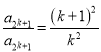 ,则
,则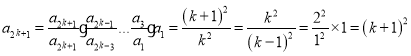 ,所以
,所以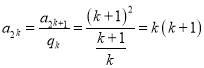 ,则
,则![]() , 故
, 故 ![]() .(ii)当
.(ii)当![]() 时,
时,![]() ,所以
,所以![]() , 则
, 则![]() , 即
, 即![]() ,得
,得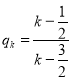 , ,则
, ,则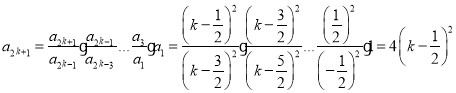 所以
所以![]() ,则
,则 ![]() ,从而
,从而![]() ,故综上所述,
,故综上所述,![]() 或
或![]() .
.

【题目】某初级中学有三个年级,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 | z | 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.