题目内容
3.函数y=|x|-2cosx的图象大致是( )| A. | 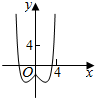 | B. | 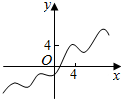 | C. | 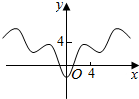 | D. | 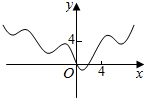 |
分析 判断函数的奇偶性,利用函数的特征,推出函数的图象即可.
解答 解:函数y=|x|-2cosx,
f(-x)=|-x|-2cos(-x)=|x|-2cosx=f(x),
函数是偶函数,排除B,D,
y=cosx是周期函数,函数y=|x|-2cosx图象具有波动性,排除A,
故选:C.
点评 本题考查函数的图象的判断,函数的奇偶性以及函数的图象的变换规律,是解题的关键.

练习册系列答案
相关题目
11.已知M={-1212,3},N=(x|mx=1},若N⊆M,则适合条件的实数m构成的集合P为( )
| A. | {-2,1313} | B. | {-1212,1313} | C. | {0,-2,1313} | D. | {0} |
14.利用斜二测画法得到的:①正三角的直观图仍是正三角形②钝角三角形的直观图仍是钝角三角形③直角三角形的直观图可能是直角三角形④直观图不会改变多边形中边的形状,以上结论正确的是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.已知f(x)={1−x−2x2x≤0|lgx|x>0若关于x的方程f(x)=a有四个实根x1,x2,x3,x4,则这四根之积x1,x2,x3,x4的取值范围是( )
| A. | [0,12) | B. | [0,14) | C. | [0,18) | D. | [0,116) |
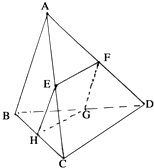 如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.
如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.