题目内容
已知数列 的前
的前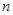 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,
(Ⅰ)求数列 的前三项
的前三项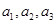 ;
;
(Ⅱ)猜想数列 的通项公式
的通项公式 ,并用数学归纳法证明
,并用数学归纳法证明
(Ⅰ)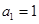 ,
,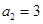 ,
,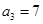 。
。
(Ⅱ)猜想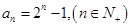 ,用数学归纳法。
,用数学归纳法。
解析试题分析:(Ⅰ)当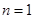 时,
时,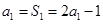 ,
,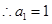
当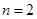 时,
时,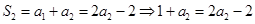 ,
,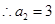
当 时,
时,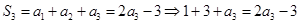 ,
,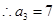
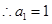 ,
,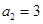 ,
,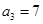 4分
4分
(Ⅱ)由(Ⅰ)猜想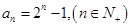 ,下面用数学归纳法证之 6分
,下面用数学归纳法证之 6分
1)当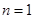 时,左边=
时,左边=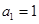 ,右边=
,右边=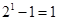 ,左边=右边,猜想成立; 8分
,左边=右边,猜想成立; 8分
2)当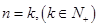 时,猜想成立,即
时,猜想成立,即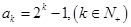 9分
9分
那么当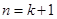 时,由已知可得
时,由已知可得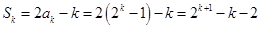
从而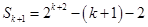
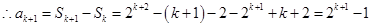
所以当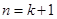 时,猜想也成立, 11分
时,猜想也成立, 11分
综上:对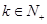 数列
数列 的通项公式为
的通项公式为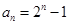 …………12分
…………12分
考点:归纳、猜想、证明,数学归纳法。
点评:中档题,本题比较典型。“归纳、猜想、证明”是发明创造的良好方法。利用数学归纳法证明过程中,要注意“两步一结”规范作答,同时,要注意应用“归纳假设”,否则,不是数学归纳法。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 满足
满足
 ,且
,且 .
.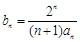 ,设数列
,设数列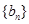 的前
的前 项和为
项和为 ,求证:
,求证: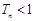 .
. 中,对于任意
中,对于任意 ,等式:
,等式: 恒成立,其中常数
恒成立,其中常数 .
. 的值;
的值;  为等比数列;
为等比数列; 的不等式
的不等式 的解集为
的解集为 ,试求实数
,试求实数 的取值范围.
的取值范围. 在函数
在函数 图象上,过点
图象上,过点 的切线的方向向量为
的切线的方向向量为 (
( >0).
>0). 的通项公式
的通项公式 ≤Sn对任意正整数n均成立,求实数
≤Sn对任意正整数n均成立,求实数 的前
的前 项和为
项和为 ,
, ,且
,且 、
、 、
、 成等差数列.
成等差数列.  是一个首项为
是一个首项为 ,公差为
,公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 .
. 是等差数列,公差
是等差数列,公差 ,
, 是
是 项和,已知
项和,已知 .
. ;
; =
= ,求数
,求数 列的前
列的前 .
. 为
为
 阶“期待数列”:
阶“期待数列”: ;②
;②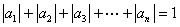 .
. 为
为 (
(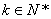 )阶“期待数列”,求公比
)阶“期待数列”,求公比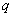 ;
;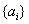 的前
的前 项和为
项和为 :
: ;
; 使
使 ,试问数列
,试问数列 能否为
能否为 ,a1=1,点
,a1=1,点 在直线
在直线 上.
上. ,求证:
,求证: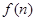 <1.
<1. 都是等差数列,且公差相等,(1)求
都是等差数列,且公差相等,(1)求 的通项公式;(2)若
的通项公式;(2)若 的前三项,记数列
的前三项,记数列 数列
数列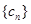 的前n项和为
的前n项和为