题目内容
已知数列 ,
, 满足:
满足: .
.
(1)若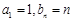 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 ,且
,且 .
.
① 记 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
② 若数列 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项 应满足的条件.
应满足的条件.
(1)
(2)①根据等差数列的定义,证明相邻两项的差为定值来得到证明。从第二项起满足题意即可。
②当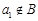
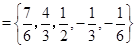 ,数列
,数列 任意一项的值均未在该数列中重复出现无数次
任意一项的值均未在该数列中重复出现无数次
解析试题分析:解:(1)当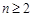 时,有
时,有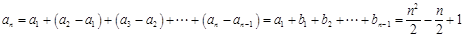 .
.
又 也满足上式,所以数列
也满足上式,所以数列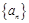 的通项公式是
的通项公式是 . 4分
. 4分
(2)①因为对任意的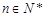 ,有
,有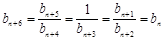 ,所以,
,所以,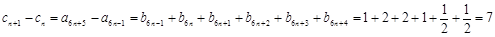 ,
,
所以,数列 为等差数列. 8分
为等差数列. 8分
②设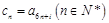 (其中
(其中 为常数且
为常数且 ,
,
所以,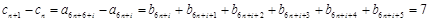 ,
,
即数列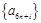 均为以7为公差的等差数列. 10分
均为以7为公差的等差数列. 10分
设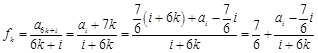 .
.
(其中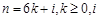 为
为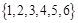 中一个常数)
中一个常数)
当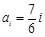 时,对任意的
时,对任意的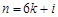 ,有
,有 ; 12分
; 12分
当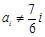 时,
时,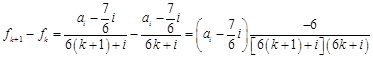 .
.
(Ⅰ)若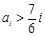 ,则对任意的
,则对任意的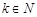 有
有 ,所以数列
,所以数列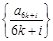 为递减数列;
为递减数列;
(Ⅱ)若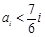 ,则对任意的
,则对任意的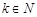 有
有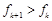 ,所以数列
,所以数列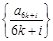 为递增数列.
为递增数列.
综上所述,集合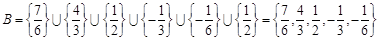 .
.
当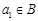 时,数列
时,数列 中必有某数重复出现无数次;
中必有某数重复出现无数次;
当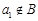 时,数列
时,数列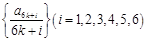 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列 任意一项的值均未在该数列中重复出现无数次. 18分
任意一项的值均未在该数列中重复出现无数次. 18分
考点:数列的性质,数列的概念
点评:主要是考查了等差数列的概念和数列的单调性的运用,属于难度题。

练习册系列答案
相关题目
 中,
中, ,
, ,若数列
,若数列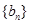 满足
满足 .
. 在函数
在函数 图象上,过点
图象上,过点 的切线的方向向量为
的切线的方向向量为 (
( >0).
>0). 的通项公式
的通项公式 ≤Sn对任意正整数n均成立,求实数
≤Sn对任意正整数n均成立,求实数 是等差数列,公差
是等差数列,公差 ,
, 是
是 项和,已知
项和,已知 .
. ;
; =
= ,求数
,求数 列的前
列的前 .
. 为
为
 阶“期待数列”:
阶“期待数列”: ;②
;②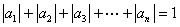 .
. 为
为 (
(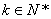 )阶“期待数列”,求公比
)阶“期待数列”,求公比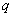 ;
;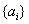 的前
的前 项和为
项和为 :
: ;
; 使
使 ,试问数列
,试问数列 能否为
能否为 和函数
和函数 ,若
,若 ,则称
,则称 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有 ,且
,且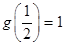 ;又数列
;又数列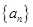 满足:
满足: .
.  是数列
是数列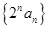 的母函数;
的母函数;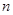 和
和 .
. 是数列
是数列 的母函数,且
的母函数,且 .若数列
.若数列 的前
的前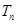 ,求证:
,求证: .
. ,a1=1,点
,a1=1,点 在直线
在直线 上.
上. ,求证:
,求证: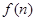 <1.
<1. }满足
}满足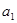 =1,
=1, =
= ,(1)计算
,(1)计算 ,
, ,
, 的值;(2)归纳推测
的值;(2)归纳推测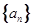 中,
中,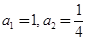 ,且
,且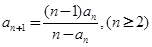 .
.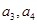 ,猜想
,猜想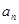 的表达式,并加以证明;
的表达式,并加以证明;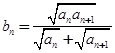 ,求证:对任意的自然数
,求证:对任意的自然数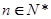 ,都有
,都有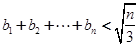 ;
;