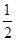题目内容
(本小题满分14分)
已知函数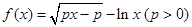 .
.
(Ⅰ)若函数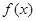 在定义域内为增函数,求实数
在定义域内为增函数,求实数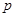 的取值范围;
的取值范围;
(Ⅱ)当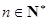 时,试判断
时,试判断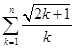 与
与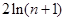 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
(Ⅲ) 当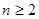 且
且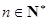 时,证明:
时,证明: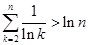 .
.
已知函数
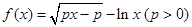 .
. (Ⅰ)若函数
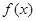 在定义域内为增函数,求实数
在定义域内为增函数,求实数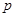 的取值范围;
的取值范围;(Ⅱ)当
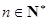 时,试判断
时,试判断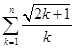 与
与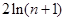 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;(Ⅲ) 当
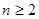 且
且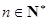 时,证明:
时,证明: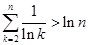 .
.(Ⅰ)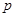 的取值范围为
的取值范围为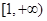 .(Ⅱ)当
.(Ⅱ)当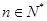 时,
时,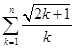
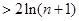 .
.
(Ⅲ)见解析.
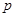 的取值范围为
的取值范围为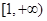 .(Ⅱ)当
.(Ⅱ)当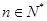 时,
时,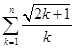
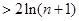 .
. (Ⅲ)见解析.
(I)求函数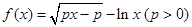 .的导数,注意定义域,令导函数大于或等于0,分离参数
.的导数,注意定义域,令导函数大于或等于0,分离参数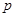 ,令一端配方求出最值即得
,令一端配方求出最值即得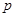 的范围;(II)由(Ⅰ)可知:
的范围;(II)由(Ⅰ)可知: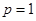 时,
时,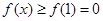 ,
,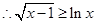 (当
(当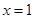 时,等号成立),令
时,等号成立),令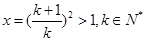 ,则
,则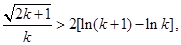 取
取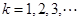 两边分别相加整理即得结论;(III)由(2)知,当
两边分别相加整理即得结论;(III)由(2)知,当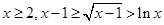 ,令
,令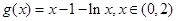 求导可得最小值
求导可得最小值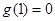 ,所以
,所以 时,
时,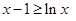 (当且仅当
(当且仅当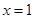 时,等号成立),令
时,等号成立),令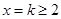 ,则
,则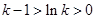 ,所以
,所以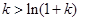 ,
,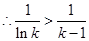 ,因而可得
,因而可得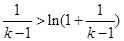 ,所以
,所以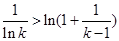 , 所以
, 所以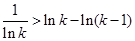 ,然后不等式累加证明即可.
,然后不等式累加证明即可.
(Ⅰ)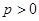 ,函数
,函数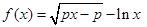 的定义域为
的定义域为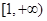 .
.
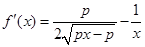 .
.
依题意,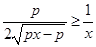 在
在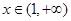 恒成立,
恒成立,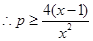 在
在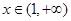 恒成立.
恒成立.
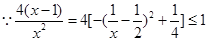 ,
,
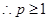 ,∴
,∴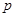 的取值范围为
的取值范围为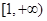 . ……………………………………………………… (4分)
. ……………………………………………………… (4分)
(Ⅱ)当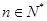 时,
时,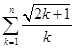
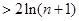 .
.
证明:当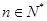 时,欲证
时,欲证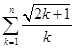
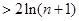 ,只需证
,只需证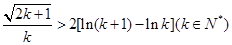 .
.
由(Ⅰ)可知:取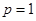 ,则
,则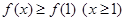 ,
,
而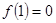 ,
,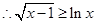 (当
(当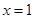 时,等号成立).
时,等号成立).
用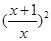 代换
代换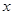 ,得
,得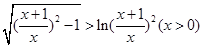 ,即
,即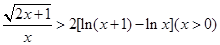 ,
,
∴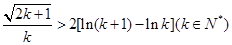 .
.
在上式中分别取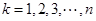 ,并将同向不等式相加,得
,并将同向不等式相加,得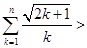
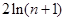 .
.
∴当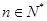 时,
时,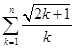
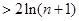 . ………………………………………… (9分)
. ………………………………………… (9分)
(Ⅲ)由(Ⅱ)可知 (
(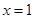 时,等号成立).
时,等号成立).
而当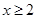 时:
时: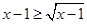 ,∴当
,∴当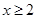 时,
时,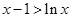 .
.
设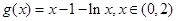 ,则
,则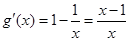 ,
,
∴ 在
在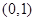 上递减,在
上递减,在 上递增,
上递增,
∴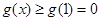 ,即
,即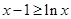 在
在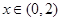 时恒成立.
时恒成立.
故当 时,
时,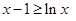 (当且仅当
(当且仅当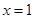 时,等号成立). …… ①
时,等号成立). …… ①
用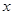 代换
代换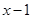 得:
得: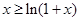 (当且仅当
(当且仅当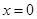 时,等号成立). …… ②
时,等号成立). …… ②
当 时,由①得
时,由①得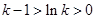 ,
,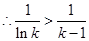 .
.
当 时,由②得
时,由②得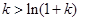 ,用
,用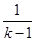 代换
代换 ,得
,得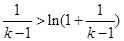 .
.
∴当 时,
时,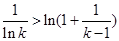 ,即
,即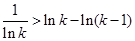 .
.
在上式中分别取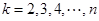 ,并将同向不等式相加,得
,并将同向不等式相加,得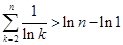 .
.
故当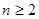 且
且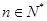 时,
时,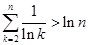 . …………………………………………………(14分)
. …………………………………………………(14分)
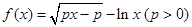 .的导数,注意定义域,令导函数大于或等于0,分离参数
.的导数,注意定义域,令导函数大于或等于0,分离参数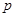 ,令一端配方求出最值即得
,令一端配方求出最值即得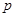 的范围;(II)由(Ⅰ)可知:
的范围;(II)由(Ⅰ)可知: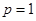 时,
时,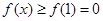 ,
,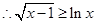 (当
(当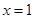 时,等号成立),令
时,等号成立),令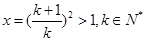 ,则
,则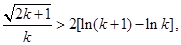 取
取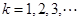 两边分别相加整理即得结论;(III)由(2)知,当
两边分别相加整理即得结论;(III)由(2)知,当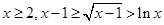 ,令
,令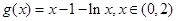 求导可得最小值
求导可得最小值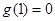 ,所以
,所以 时,
时,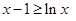 (当且仅当
(当且仅当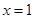 时,等号成立),令
时,等号成立),令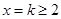 ,则
,则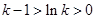 ,所以
,所以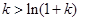 ,
,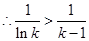 ,因而可得
,因而可得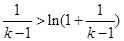 ,所以
,所以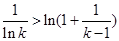 , 所以
, 所以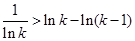 ,然后不等式累加证明即可.
,然后不等式累加证明即可.(Ⅰ)
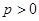 ,函数
,函数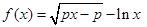 的定义域为
的定义域为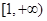 .
.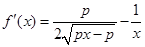 .
.依题意,
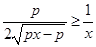 在
在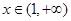 恒成立,
恒成立,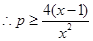 在
在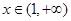 恒成立.
恒成立.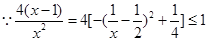 ,
,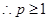 ,∴
,∴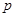 的取值范围为
的取值范围为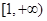 . ……………………………………………………… (4分)
. ……………………………………………………… (4分)(Ⅱ)当
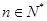 时,
时,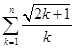
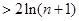 .
.证明:当
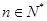 时,欲证
时,欲证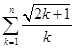
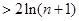 ,只需证
,只需证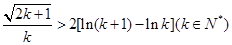 .
.由(Ⅰ)可知:取
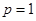 ,则
,则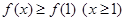 ,
,而
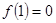 ,
,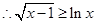 (当
(当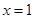 时,等号成立).
时,等号成立).用
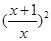 代换
代换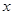 ,得
,得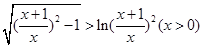 ,即
,即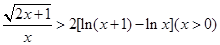 ,
,∴
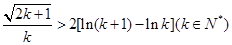 .
.在上式中分别取
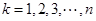 ,并将同向不等式相加,得
,并将同向不等式相加,得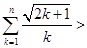
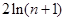 .
.∴当
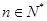 时,
时,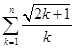
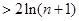 . ………………………………………… (9分)
. ………………………………………… (9分)(Ⅲ)由(Ⅱ)可知
 (
(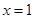 时,等号成立).
时,等号成立).而当
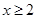 时:
时: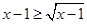 ,∴当
,∴当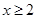 时,
时,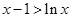 .
.设
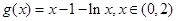 ,则
,则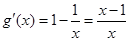 ,
,∴
 在
在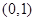 上递减,在
上递减,在 上递增,
上递增,∴
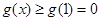 ,即
,即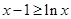 在
在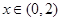 时恒成立.
时恒成立.故当
 时,
时,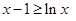 (当且仅当
(当且仅当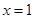 时,等号成立). …… ①
时,等号成立). …… ①用
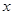 代换
代换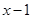 得:
得: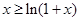 (当且仅当
(当且仅当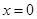 时,等号成立). …… ②
时,等号成立). …… ②当
 时,由①得
时,由①得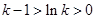 ,
,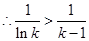 .
. 当
 时,由②得
时,由②得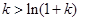 ,用
,用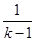 代换
代换 ,得
,得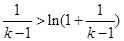 .
.∴当
 时,
时,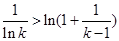 ,即
,即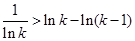 .
.在上式中分别取
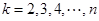 ,并将同向不等式相加,得
,并将同向不等式相加,得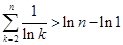 .
.故当
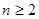 且
且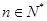 时,
时,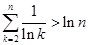 . …………………………………………………(14分)
. …………………………………………………(14分)
练习册系列答案
相关题目

 的单调区间;
的单调区间; ,求相应的值。
,求相应的值。 上的函数
上的函数 ,
,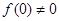 ,当
,当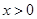 时,
时,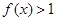 ,且对任意的
,且对任意的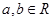 ,有
,有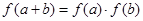 ,
,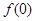 的值;
的值;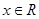 ,恒有
,恒有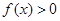 ;
;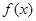 的单调性,并证明你的结论。
的单调性,并证明你的结论。 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。 是定义在
是定义在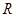 上的奇函数,且当
上的奇函数,且当 时,
时, 。若对任意的
。若对任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数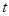 的取值范围是 。
的取值范围是 。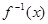 ,且对于任意的
,且对于任意的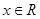 ,恒有f(x)+f(-x)=1,则
,恒有f(x)+f(-x)=1,则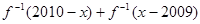 =( )
=( ) ,
,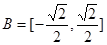 ,函数
,函数 ,
,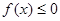 的解集为C,当
的解集为C,当 时,求实数
时,求实数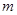 取值范围;
取值范围; ,都有
,都有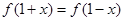 成立,试求
成立,试求 时,
时,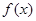 的值域;
的值域;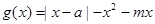
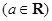 ,求
,求 的最小值.
的最小值. 在区间
在区间 上的最大值是
上的最大值是