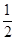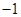题目内容
已知函数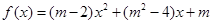 是偶函数,
是偶函数,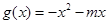 在
在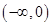 内单调递增,则实数
内单调递增,则实数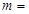 ( )
( )
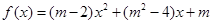 是偶函数,
是偶函数,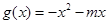 在
在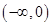 内单调递增,则实数
内单调递增,则实数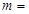 ( )
( )A.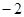 | B.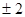 | C.0 | D.2 |
D
解:函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,可得m2-4=0,故m=±2,①
又由函数g(x)=x3+2x2+mx+5在(-∞,+∞)内单调递增,得出
g'(x)=3x2+4x+m≥0在R上恒成立,故△≤0,即16-12m≤0,即m≥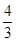 ②
②
由①②得m=2
故选D
又由函数g(x)=x3+2x2+mx+5在(-∞,+∞)内单调递增,得出
g'(x)=3x2+4x+m≥0在R上恒成立,故△≤0,即16-12m≤0,即m≥
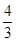 ②
②由①②得m=2
故选D

练习册系列答案
相关题目
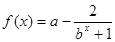
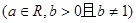
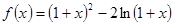 .(1)求
.(1)求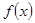 的单调区间;(2)当
的单调区间;(2)当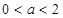 时,求函数
时,求函数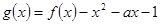 在区间
在区间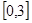 上的最小值.
上的最小值.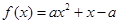 .
.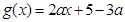
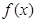 在
在 上的最大值是
上的最大值是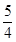 ,求
,求 的值;
的值; 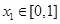 ,总存在
,总存在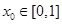 ,使得
,使得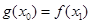 成立,求
成立,求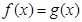 在
在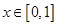 上有解,求
上有解,求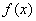 是定义在
是定义在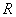 上的偶函数,在
上的偶函数,在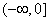 上是增函数,则使得
上是增函数,则使得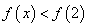 的
的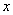 取值范围是( )
取值范围是( )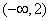
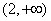
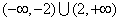
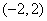
 上的函数
上的函数 满足:①
满足:① 是奇函数;②当
是奇函数;②当 时,函数
时,函数 ,则
,则 的值( )
的值( ) 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。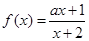 在区间
在区间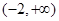 上是增函数,则
上是增函数,则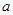 的取值范围是 .
的取值范围是 . 在
在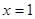 处取到极值,则
处取到极值,则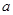 的值为 ( )
的值为 ( )