题目内容
12.已知A={x|y=x2-2x+1},B={y|y=x2-2x+1},C={x|x2-2x+1=0},D={x|x2-2x+1<0},E={(x,y)|y=x2-2x+1},F={(x,y)|x2-2x+1=0,y∈R},则下面结论正确的是( )| A. | A⊆B⊆C⊆D | B. | D?C?B?A | C. | E=F | D. | A=B=E |
分析 化简六个集合,明确其含义,即可得出结论.
解答 解:A={x|y=x2-2x+1}代表y=x2-2x+1中的取值范围,故A=R.
B={y|y=x2-2x+1}代表y=x2-2x+1中的取值范围,故B={y|y≥0}.
C={x|x2-2x+1=0}代表x2-2x+1=0的根的组成的集合,故C={1}.
D={x|x2-2x+1<0}代表不等式x2-2x+1<0的解集,故D=∅.
E={(x,y)|y=x2-2x+1}代表抛物线y=x2-2x+1上的点组成的点集.
F={(x,y)|x2-2x+1=0,y∈R}代表直线x=1上的点组成的点集.
故选:B.
点评 此题给的六个集合的元素特征均与x2-2x+1有关,因此,很容易错选集合的元素.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.原命题为“对于函数f(x)=ax2+bx+c(a>0),x∈(m,n)时,若f(x)<0,则$\left\{\begin{array}{l}{f(m)<0}\\{f(n)<0}\end{array}\right.$”关于其逆命题,否命题,逆否命题真假性的判断依次为( )
| A. | 真,真,真 | B. | 假,假,真 | C. | 真,真,假 | D. | 假,假,假 |
7.已知全集U={1,2,a2-2a+3},A=(1,a),∁UA={3},则实数a等于( )
| A. | 0或2 | B. | 0 | C. | 1或2 | D. | 2 |
5.如图所示,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=1,AB的中点是C,则$\overrightarrow{OC}$的坐标是( )
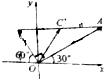

| A. | ($\frac{\sqrt{3}}{4}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | B. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{2}$,$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$) | C. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | D. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$) |