题目内容
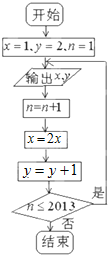
根据程序框图,将输出的x,y值依次分别记为x1,x2,…,x2013;y1,y2,…,y2013
(Ⅰ)写出数列{xn}的递推公式,求{xn}的通项公式;
(Ⅱ)写出数列{yn}的递推公式,求{yn}的通项公式;
(Ⅲ)求数列{xn+yn}的前n项和Sn(n≤2013).
(Ⅰ)写出数列{xn}的递推公式,求{xn}的通项公式;
(Ⅱ)写出数列{yn}的递推公式,求{yn}的通项公式;
(Ⅲ)求数列{xn+yn}的前n项和Sn(n≤2013).

(Ⅰ)数列{xn}的递推公式为xn+1=2xn,
∵
=2,
∴数列{xn}构成一个首项为1公比为2的等比数列,
∴数列{xn}的通项公式为xn=2n-1(n≤2013);
(Ⅱ)数列{yn}的递推公式为yn+1=yn+1,
证明:∵yn+1-yn=1,
∴{yn}是首项为2公差为1的等差数列,
∴yn=y1+(n-1)×1=n+1,
即数列{yn}的通项公式为yn=n+1(n≤2013);
(Ⅲ)由(Ⅰ)(Ⅱ)知xn+yn=2n-1+(n+1),
∴Sn=(20+21+22+…+2n-1)+[2+3+4+…+(n+1)]
=
+
=2n-1+
(n≤2013).
∵
| xn+1 |
| xn |
∴数列{xn}构成一个首项为1公比为2的等比数列,
∴数列{xn}的通项公式为xn=2n-1(n≤2013);
(Ⅱ)数列{yn}的递推公式为yn+1=yn+1,
证明:∵yn+1-yn=1,
∴{yn}是首项为2公差为1的等差数列,
∴yn=y1+(n-1)×1=n+1,
即数列{yn}的通项公式为yn=n+1(n≤2013);
(Ⅲ)由(Ⅰ)(Ⅱ)知xn+yn=2n-1+(n+1),
∴Sn=(20+21+22+…+2n-1)+[2+3+4+…+(n+1)]
=
| 1×(1-2n) |
| 1-2 |
| n(n+3) |
| 2 |
=2n-1+
| n2+3n |
| 2 |

练习册系列答案
相关题目
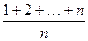 ,bn=
,bn=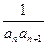 ,则{bn}的前n项
,则{bn}的前n项