Question

【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地，目前德国汉堡，美国波士顿等申办城市因市民担心赛事费用超支而相继退出，某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：

	支持	不支持	合计
年龄不大于50岁			80
年龄大于50岁	10
合计		70	100

（1）根据已知数据，把表格数据填写完整；

（2）能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关？

（3）已知在被调查的年龄大于50岁的支持者中有6名女性，其中2名是女教师．现从这6名女性中随机抽取2名，求恰有1名女教师的概率．

附：，，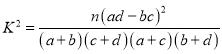

	0.100	0.050	0.025	0.010
	2.706	3.841	5.024	6.635

Answer 1

【答案】（1）表格见解析；（2）能在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关；（3）.

【解析】

（1）根据已知数据即可填表.

（2）根据列联表求出观测值，再根据独立性检验的基本思想即可求解.

（3）记6人为，其中表示教师，列出基本事件个数，再根据古典概型的概率计算公式即可求解.

（1）

	支持	不支持	合计
年龄不大于50岁	20	60	80
年龄大于50岁	10	10	20
合计	30	70	100

（2），

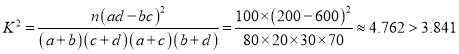所以能在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关；

（3）记6人为，其中表示教师，

从6人任意抽2人的所有等可能事件是：，，，，，

，，，，，，，，，共15个，

其中恰有1位教师有8个基本事件：，，，，，，，，

所以所求概率是．