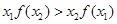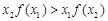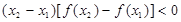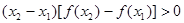题目内容
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)过点(0,1)作直线l1与l垂直,且直线l1与圆C交于M、N两点,求四边形PMQN面积的最大值.
(1)求圆C的方程;
(2)过点(0,1)作直线l1与l垂直,且直线l1与圆C交于M、N两点,求四边形PMQN面积的最大值.
(1)x2+y2=4 (2)7
(1)设圆心C(a,a),半径为r,因为圆C经过点A(-2,0),B(0,2),
所以|AC|=|BC|=r,即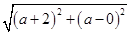 =
=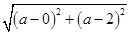 =r,解得a=0,r=2.
=r,解得a=0,r=2.
故所求圆C的方程为x2+y2=4.
(2)设圆心C到直线l,l1的距离分别为d,d1,四边形PMQN的面积为S.
因为直线l,l1都经过点(0,1),且l1⊥l,根据勾股定理,有d12+d2=1.
又|PQ|=2×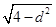 ,|MN|=2×
,|MN|=2×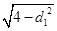 ,
,
所以S=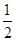 |PQ|·|MN|,
|PQ|·|MN|,
即S=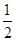 ×2×
×2×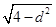 ×2×
×2×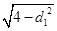 =
=
2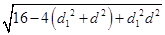 =2
=2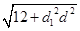 ≤
≤
2 =2
=2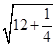 =7,
=7,
当且仅当d1=d时,等号成立,所以四边形PMQN面积的最大值为7.
所以|AC|=|BC|=r,即
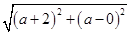 =
=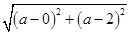 =r,解得a=0,r=2.
=r,解得a=0,r=2.故所求圆C的方程为x2+y2=4.
(2)设圆心C到直线l,l1的距离分别为d,d1,四边形PMQN的面积为S.
因为直线l,l1都经过点(0,1),且l1⊥l,根据勾股定理,有d12+d2=1.
又|PQ|=2×
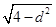 ,|MN|=2×
,|MN|=2×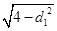 ,
,所以S=
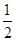 |PQ|·|MN|,
|PQ|·|MN|,即S=
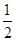 ×2×
×2×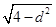 ×2×
×2×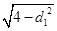 =
=2
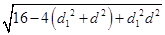 =2
=2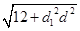 ≤
≤2
 =2
=2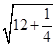 =7,
=7,当且仅当d1=d时,等号成立,所以四边形PMQN面积的最大值为7.

练习册系列答案
相关题目
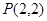 ,圆
,圆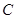 :
: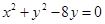 ,过点
,过点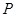 的动直线
的动直线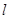 与圆
与圆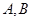 两点,线段
两点,线段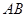 的中点为
的中点为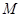 ,
,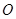 为坐标原点.
为坐标原点.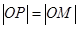 时,求
时,求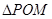 的面积
的面积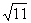 为半径的圆
为半径的圆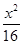 -
-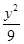 =1的两条渐近线都相切的圆的方程为________.
=1的两条渐近线都相切的圆的方程为________.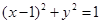 上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若
上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若 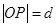 ,则函数
,则函数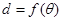 的大致图像是 ( )
的大致图像是 ( )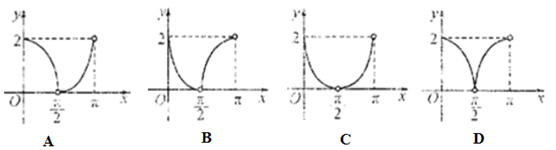
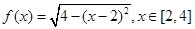 对于满足
对于满足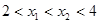 的任意
的任意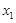 ,
,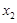 ,给出下列结论:
,给出下列结论: