Question

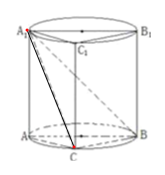
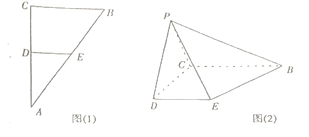
【题目】已知Rt△ABC如图（1），∠C＝90°，D.E分别是AC，AB的中点，将△ADE沿DE折起到PDE位置（即A点到P点位置）如图（2）使∠PDC＝60°．

（1）求证：BC⊥PC；

（2）若BC＝2CD＝4，求点D到平面PBE的距离．

Answer 1

【答案】（1）见解析；（2）

【解析】

(1)证明垂直平面中的两条直线再证明平面即可.

(2)取取CD中点建立空间直角坐标系,再利用空间向量解决点到面的距离问题即可.

（1）证明：∵Rt△ABC如图（1），∠C＝90°，D.E分别是AC，AB的中点，

将△ADE沿DE折起到PDE位置（即A点到P点位置）如图（2）使∠PDC＝60°．

∴DE⊥DC，DE⊥PD，DE∥BC，

∵PD∩DC＝D，∴DE⊥平面PCD，∴BC⊥平面PCD，

∵PC平面PCD，∴BC⊥PC.

（2）解：∵D.E分别是AC，AB的中点，∠PDC＝60°，BC＝2CD＝4，

∴CD＝PD＝PC＝2，

取CD中点O，BE中点M，连结PO，MO，则OP，OD，OM两两垂直，

以O为原点，OD为x轴，OM为y轴，OP为z轴，建立空间直角坐标系，

则D（1，0，0），P（0，0，），B（﹣1，4，0），E（1，2，0），

（1，0，），（﹣1，4，），（1，2，），

设平面PBE的法向量（x，y，z），

则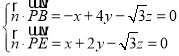，取x＝1，得（1，1，），

∴点D到平面PBE的距离为：

d．