题目内容
18.已知直线l与双曲线x2-y2=1交于A、B两点,若线段AB的中点为C(2,1),则直线l的斜率为( )| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
分析 设出A,B的坐标,代入双曲线方程,作差后利用中点坐标公式代入即可求得直线l的斜率.
解答 解:设A(x1,y1),B(x2,y2),
∵A,B在双曲线上,∴${{x}_{1}}^{2}-{{y}_{1}}^{2}=1$,${{x}_{2}}^{2}-{{y}_{2}}^{2}=1$,
两式作差可得:${{x}_{1}}^{2}-{{x}_{2}}^{2}={{y}_{1}}^{2}-{{y}_{2}}^{2}$,即(x1-x2)(x1+x2)=(y1-y2)(y1+y2),
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,
∵线段AB的中点为C(2,1),∴x1+x2=4,y1+y2=2,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=\frac{4}{2}=2$.
即直线l的斜率为2.
故选:C.
点评 本题考查直线与圆锥曲线的位置关系,训练了“点差法”求直线的斜率,涉及中点弦问题,常采用这种方法,是中档题.

练习册系列答案
相关题目
10.设椭圆C的两个焦点分别为F1、F2,若C上存在点P满足|PF1|:|F1F2|:|PF2|=4:3:2,则C的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
7.若非零向量$\vec a$与向量$\vec b$的夹角为钝角,$|{\vec b}|=2$,且当t=-2时,$|{\vec b-t\vec a}|$(t∈R)取最小值$\frac{6}{5}$,则$\vec a•({\vec b-\vec a})$等于( )
| A. | $-\frac{48}{25}$ | B. | -2 | C. | $-\frac{11}{5}$ | D. | $\frac{9}{5}$ |
8.已知a,b∈R+,则$\frac{{\sqrt{{a^3}b}}}{{\root{3}{ab}}}$=( )
| A. | ${a^{\frac{1}{6}}}{b^{\frac{7}{6}}}$ | B. | ${a^{\frac{7}{6}}}{b^{\frac{1}{6}}}$ | C. | ${a^{\frac{1}{3}}}{b^{\frac{1}{6}}}$ | D. | ${a^{\frac{1}{2}}}{b^{\frac{1}{6}}}$ |
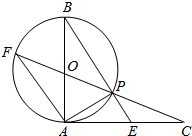 如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.