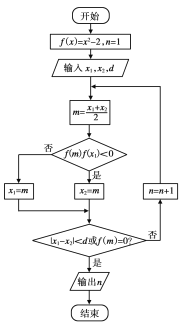
题目内容
【题目】设
：实数
满足不等式
， 
：函数
无极值点.
（1）若“
”为假命题，“
”为真命题，求实数
的取值范围；
（2）已知“
”为真命题，并记为
，且
： 
，若
是
的必要不充分条件，求正整数
的值．
【答案】（1）
；（2）
.
【解析】试题分析：由
，得
；函数
无极值点， 
恒成立，得
，解得
．（1）“
”为假命题，“
”为真命题，则
与
只有一个命题是真命题，分成
真
假和
假
真两类来求
的取值范围；（2）“
”为真命题，两个都是真命题，所以
．将
因式分解得
，解得
或
， 
， 
是
的必要不充分条件得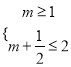
，解得
，所以
．
试题解析：
由
，得
，即
．．．．．．．．．．．．．．．．1分
∵函数
无极值点，∴
恒成立，得
，解得
，
即
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
（1）∵“
”为假命题，“
”为真命题，∴
与
只有一个命题是真命题．
若
为真命题， 
为假命题，则
；．．．．．．．．．．．．．．．．．．．．．5分
若
为真命题， 
为假命题，则
．．．．．．．．．．．．．．6分
于是，实数
的取值范围为
．．．．．．．．．．．．．．．．．．．．．7分
（2）∵“
”为真命题，∴
．．．．．．．．．．．．．．8分
又
，
∴
，
∴
或
，．．．．．．．．．．．．．．．．．．．10分
即
或
，从而
，
∵
是
的必要不充分条件，即
是
的充分不必要条件，
∴
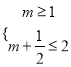，解得
，∵
，∴
．．．．．．．．．．．．．．．．．．12分
【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
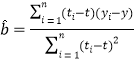【题目】心理学家分析发现“喜欢空间想象”与“性别”有关，某数学兴趣小组为了验证此结论，从全体组员中按分层抽样的方法抽取50名同学（男生30人、女生20人），给每位同学立体几何题、代数题各一道，让各位同学自由选择一道题进行解答，选题情况统计如下表：（单位：人）
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
（1）能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关？
（2）经统计得，选择做立体几何题的学生正答率为
，且答对的学生中男生人数是女生人数的5倍，现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究，求恰好抽到男女生各一人的概率．
附表及公式：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
