Question

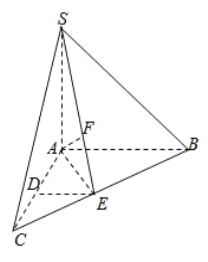
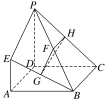
【题目】如图，在长方体中，是的中点，点是上一点，，，.动点在上底面上，且满足三棱锥的体积等于1，则直线与所成角的正切值的最大值为（ ）

A.B.C.D.2

Answer 1

【答案】A

【解析】

先证明，

在证明平面平面，即可找到动点的轨迹是线段，最后求最大值即可．

解：

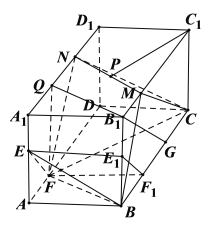
在上取点、，使,

在上取点，使,

因为是的中点,，

所以，所以四边形是平行四边形，所以

同理可证四边形是平行四边形，所以

所以，四边形是平行四边形，

所以，又

在上取点，使，则，四边形是平行四边形

所以

平面

平面

在上取点，使，则，

四边形是平行四边形，所以

显然，所以，

平面

平面

又平面，平面，

平面平面，

，

又动点在上底面上

动点在线段

∴当点在上运动时，满足三棱锥的体积等于1，

又直线与所成角就是直线与所成角，

即为所求，

∴当点与重合时，取最大值，

即.

故选：A