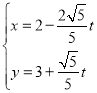题目内容
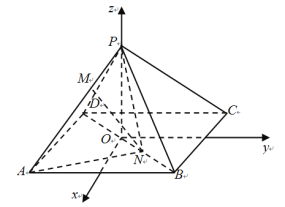
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
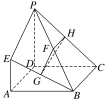
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)通过证明BC⊥平面ABE,FH∥BC,证得FH⊥平面ABE,即可证得面面垂直;
(2)建立空间直角坐标系,利用向量方法求线面角的正弦值.
(1)由题:,AE⊥平面ABCD,BC![]() 平面ABCD,所以AE⊥BC,
平面ABCD,所以AE⊥BC,
四边形ABCD是正方形,AB⊥BC,AE与AB是平面ABE内两条相交直线,
所以BC⊥平面ABE,F,H分别为BP,PC的中点,所以FH∥BC,
所以FH⊥平面ABE,HF![]() 平面GHF,所以平面ABE⊥平面GHF;
平面GHF,所以平面ABE⊥平面GHF;
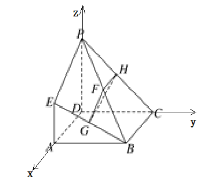
(2)由题可得:DA,DC,DP两两互相垂直,所以以D为原点,DA,DC,DP为x,y,z轴的正方向建立空间直角坐标系如图所示:
![]() ,
,
所以![]() ,设平面PBC的法向量
,设平面PBC的法向量![]() ,
,
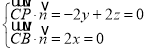 ,取
,取![]() 为平面PBC的一个法向量,
为平面PBC的一个法向量,
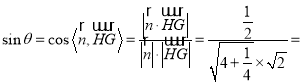
![]()
所以直线GH与平面PBC所成的角θ的正弦值![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目