��Ŀ����
����Ŀ��Ϊ���С��¿��á���ѧ����ij��ѧ��ʦ�ֱ��ô�ͳ��ѧ�͡��¿��á����ֲ�ͬ�Ľ�ѧ��ʽ���ڼס�������ƽ�а���н�ѧʵ�飬Ϊ�˽��ѧЧ�������п��Ժֱ�������༶�и������ȡ![]() ��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ����ͼ���dzɼ�������
��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ����ͼ���dzɼ�������![]() ����Ϊ���ɼ�������.
����Ϊ���ɼ�������.

��1���ֱ����ס�������![]() �������У���ѧ����ǰʮ��ƽ���֣����ݴ��ж����ֽ�ѧ��ʽ�Ľ�ѧЧ����
�������У���ѧ����ǰʮ��ƽ���֣����ݴ��ж����ֽ�ѧ��ʽ�Ľ�ѧЧ����
�ѣ�
��2���ס�������![]() �������У��ɼ���
�������У��ɼ���![]() �����£�����
�����£�����![]() �֣���ѧ��������ѡȡ
�֣���ѧ��������ѡȡ![]() �ˣ�����
�ˣ�����![]() �����Բ�ͬ�༶�ĸ��ʣ�
�����Բ�ͬ�༶�ĸ��ʣ�
��3��������ͳ��������д����![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����
�����������ж��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء�?
��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء�?
�װ� | �Ұ� | �ܼ� | |
�ɼ����� | |||
�ɼ������� | |||
�ܼ� |
���� 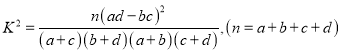
�����Լ����ٽ�ֵ����
|
|
|
|
|
|
|
|
|
|
���𰸡���1����Ч���ø��ѣ���2�� ![]() ����3����.
����3����.
�������������������1�������⣬�ɸ��ݾ�Ҷͼ���ṩ���ݣ��Լ����������ȡǰ10���ķ�������������ƽ��ֵ���ɣ��ɴ˿��жϸ�Ч���ø��ѣ���2���ɾ�Ҷͼͳ��������60�����µ��������ٰ��ŵ�����ʵļ��㹫ʽ�������㼴�ɣ���3���������⣬�ɾ�Ҷͼͳ���������е����������ݹ�ʽ���![]() ���ٱȶ��ٽ�ֵ�����Ӷ��ɵó�����.
���ٱȶ��ٽ�ֵ�����Ӷ��ɵó�����.
�����������1���װ�������ѧ�ɼ�ǰʮ��ƽ����Ϊ
![]() ��
��
�Ұ�������ѧ�ɼ�ǰʮ��ƽ����Ϊ
![]() ��
��
�װ�������ѧ�ɼ�ǰʮ��ƽ����Զ�����Ұ�������ѧ�ɼ�ǰʮ��ƽ���֣����¿����жϡ���Ч���á���ѧ��ʽ�Ľ�ѧЧ������.
��2�������гɼ�![]() �����µ�ѧ���мװ���
�����µ�ѧ���мװ���![]() �ˣ���Ϊ��
�ˣ���Ϊ�� ![]() ���Ұ���
���Ұ���![]() �ˣ���Ϊ��
�ˣ���Ϊ�� ![]() .
.
���![]() ��
�� ![]() ����Ԫ��������ѡ
����Ԫ��������ѡ![]() �������л����¼����£�
�������л����¼����£�
![]() ��һ����
��һ����![]() �������¼���
�������¼���
��![]() ��ʾ����
��ʾ����![]() �����Բ�ͬ�༶�������£�
�����Բ�ͬ�༶�������£�
![]() ��һ����
��һ����![]() �������¼���
�������¼���
����![]() .
.
��3��
�װ� | �Ұ� | �ܼ� | |
�ɼ����� |
|
|
|
�ɼ������� |
|
|
|
�ܼ� |
|
|
|
����![]() �������е����ݣ���
�������е����ݣ���![]() �Ĺ۲�ֵΪ
�Ĺ۲�ֵΪ
![]() ��
��
�����ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء�.
��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء�.

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�����Ŀ��ij��ȤС�����о���ҹ�²��С�뻼��ð��������֮��Ĺ�ϵ,���Ƿֱ��������ijҽԺ��¼�� 1��6�·�ÿ��10�ŵ���ҹ�²��������ð�����������,�õ��������ϣ�
�� �� | 1��10�� | 2��10�� | 3��10�� | 4��10�� | 5��10�� | 6��10�� |
��ҹ�²�x(��C) | 10 | 11 | 13 | 12 | 8 | 6 |
��������y(��) | 22 | 25 | 29 | 26 | 16 | 12 |
����ȤС��ȷ�����о�������:�ȴ�������������ѡȡ2��,��ʣ�µ�4�����������Իع鷽��,���ñ�ѡȡ��2�����ݽ��м��飮
(1)��ѡȡ��2������ǡ�������������µĸ��ʣ�
(2)��ѡȡ����1����6�µ���������,�����2��5�·ݵ�����,���y����x�����Իع鷽��![]() ��
��
(3)�������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2��,����Ϊ�õ������Իع鷽���������,���ʸ�С���������Իع鷽���Ƿ�����?
���ο�:����С���˷������Իع鷽��ϵ����ʽ 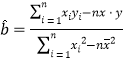 ��
��![]() ��
��