题目内容
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了 1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考:用最小二乘法求线性回归方程系数公式 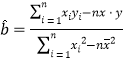 ,
,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)该小组所得线性回归方程是理想的.
;(3)该小组所得线性回归方程是理想的.
【解析】试题分析:(1)由列举法可得从6组数据中选取2组数据共有15种情况, 抽到相邻两个月的数据的情况有5种,由古典概型概率公式可得结果;(2)由公式  求出
求出![]() 的值,将样本中心点的坐标代入回归方程可得
的值,将样本中心点的坐标代入回归方程可得![]() 的值,从而可得结果;(3)根据
的值,从而可得结果;(3)根据![]() 时与
时与
![]() 时,由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,即可得结果.
时,由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,即可得结果.
试题解析:(1)设抽到相邻两个月的数据为事件A.
因为从6组数据中选取2组数据共有15种情况,
每种情况都是等可能出现的其中,抽到相邻两个月的数据的情况有5种,
所以![]()
(2) 由数据求得![]() , 由公式求得
, 由公式求得![]()
再由![]() ,
,
所以关于的线性回归方程为![]()
(3)当![]() 时,
时,![]() ,
, ![]() ;
;
同样, 当![]() 时,
时,![]() ,
, ![]()
所以,该小组所得线性回归方程是理想的.
【方法点晴】本题主要考查古典概型概率公式和线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.