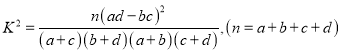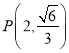题目内容
【题目】如图，一架飞机以600km/h的速度，沿方位角60°的航向从A地出发向B地飞行，飞行了36min后到达E地，飞机由于天气原因按命令改飞C地，已知AD=600 
km，CD=1200km，BC=500km，且∠ADC=30°，∠BCD=113°．问收到命令时飞机应该沿什么航向飞行，此时E地离C地的距离是多少？（参考数据：tan37°= 
） 
【答案】解：连接AC，CE，在△ACD中由余弦定理，得： 
，
∴AC=600，
则CD2=AD2+AC2 ， 即△ACD是直角三角形，且∠ACD=60°，
又∠BCD=113°，则∠ACB=53°，
∵tan37°= 
，
∴cos53°=sin37°= ．
在△ABC中，由余弦定理，得： 
，则AB=500，
又BC=500，则△ABC是等腰三角形，且∠BAC=53°，
由已知有 
，
在△ACE中，由余弦定理，有 
，
又AC2=AE2+CE2 ， 则∠AEC=90°．
由飞机出发时的方位角为600 ， 则飞机由E地改飞C地的方位角为：90°+60°=150°．
答：收到命令时飞机应该沿方位角150°的航向飞行，E地离C地480km．
【解析】在△ACD中使用余弦定理得出AC及∠ACD，在△ABC中使用余弦定理得出AB及∠CAE，再在△ACE中使用余弦定理得出CE及∠AEC．
练习册系列答案
阅读快车系列答案
相关题目
