题目内容
17.已知f(x)=$\left\{\begin{array}{l}{2x+1,}&{x≤0}\\{{x}^{2}-1,}&{x>0}\end{array}\right.$,则“f[f(a)]=1“是“a=1”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
分析 根据充分条件和必要条件的定义,结合函数的性质进行判断即可.
解答 解:当a=1,则f(a)=f(1)=0,则f(0)=0+1=1,则必要性成立,
若x≤0,若f(x)=1,则2x+1=1,则x=0,
若x>0,若f(x)=1,则x2-1=1,则x=$\sqrt{2}$,
即若f[f(a)]=1,则f(a)=0或$\sqrt{2}$,
若a>0,则由f(a)=0或1得a2-1=0或a2-1=$\sqrt{2}$,
即a2=1或a2=$\sqrt{2}$+1,解得a=1或a=$\sqrt{1+\sqrt{2}}$,
若a≤0,则由f(a)=0或1得2a+1=0或2a+1=$\sqrt{2}$,
即a=-$\frac{1}{2}$,此时充分性不成立,
即“f[f(a)]=1“是“a=1”的必要不充分条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,根据分段函数的表达式解方程即可.

练习册系列答案
相关题目
7.在区域$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$内任意取一点P(x,y),则点P到原点距离小于1的概率是( )
| A. | 0 | B. | $\frac{π}{4}$-$\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
8.设函数f(x)=sin(ωx+φ)+$\sqrt{3}$cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)与直线y=2的相邻两个交点的距离为π,且f(x)-f(-x)=0,若g(x)=sin(ωx+φ),则( )
| A. | y=g(x)在(0,$\frac{π}{2}$)上递减 | B. | y=g(x)在(0,$\frac{π}{6}$)上递减 | ||
| C. | y=g(x)在(0,$\frac{π}{2}$)上递增 | D. | y=g(x)在(0,$\frac{π}{6}$)上递增 |
12.已知程序框图如图所示,则该程序框图的功能是( )


| A. | 求数列{$\frac{1}{n}$}的前11项和(n∈N*) | B. | 求数列{$\frac{1}{2n}$}的前11项和(n∈N*) | ||
| C. | 求数列{$\frac{1}{n}$}的前12项和(n∈N*) | D. | 求数列{$\frac{1}{2n}$的前12项和(n∈N*) |
9.已知直线3x+ay=0(a>0)被圆(x-2)2+y2=4所截得的弦长为2,则a的值为( )
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$,|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2$\sqrt{3}$且$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$垂直,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
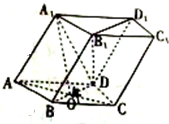 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.