题目内容
【题目】已知函数
.
（1）判断
的单调性并写出证明过程；
（2）当
时，关于x的方程
在区间
上有唯一实数解，求a的取值范围.
【答案】（1）
在R上递增，证明见解析；（2）
或
.
【解析】
（1）先判断函数的奇偶性，再根据函数单调性的定义，作差比较大小即可求证明；
（2）根据（1）中所求单调性，将问题转化为
的零点问题，利用
之间的关系进行换元，转化为二次函数零点的分布问题即可求得.
（1）在R上递增.
证明：
，
恒成立，
的定义域为R.
令
，
，
是奇函数.
令
，
，
，
在
上递增，又
是R上连续不断的奇函数，
在R上递增.
（2）由（1）得
且在R上递增.
整理得
，在
上有唯一实数解
构造，，
.
令
，则
，
，
在
内有且只有一个零点，
无零点.
又
，
在
上为增函数.
ⅰ）若
在内有且只有一个零点，无零点.
则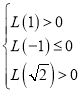
ⅱ）若
为的零点，无零点，
则
，
又，经检验符合题意.
综上所述：
或.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活，创建了社区“文化丹青”大型活动场所，配备了各种文化娱乐活动所需要的设施，让广大居民健康生活、积极向上．社区最近四年内在“文化丹青”上的投资金额统计数据如表：（为了便于计算，把2015年简记为5，其余以此类推）
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
（1）利用所给数据，求出投资金额
与年份
之间的回归直线方程
；
（2）预测该社区在2019年在“文化丹青”上的投资金额．
（附：对于一组数据
， 
，…， 
，其回归直线
的斜率和截距的最小二乘估计分别为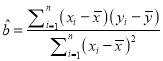
， 
．）
