题目内容
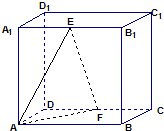
如图,正方体AC1
(1)在BD上确定一点E,使D1E∥面A1C1B;
(2)求直线BB1和面A1C1B所成角的正弦值;
(3)求面A1C1B与底面ABCD所成二面角的平面角的正弦值.
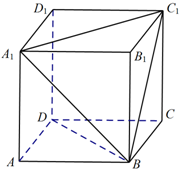
(1)在BD上确定一点E,使D1E∥面A1C1B;
(2)求直线BB1和面A1C1B所成角的正弦值;
(3)求面A1C1B与底面ABCD所成二面角的平面角的正弦值.

(1)连接AC,B1D1,AC∩BD=O,A1C1∩B1D1=O1,连接D1O,O1B,则
∵D1O1=BO,D1O1∥BO,∴四边形D1OBO1是平行四边形,
∴D1O∥O1B
∵D1O?平面A1C1B,O1B?平面A1C1B,
∴D1O∥面A1C1B;
∴BD上存在中点E,使D1E∥面A1C1B;
(2)连接B1D,则B1D⊥面A1C1B,设垂足为G,则∠GBB1为直线BB1和面A1C1B所成角
∵B1G=
B1D=
BB1,
∴直线BB1和面A1C1B所成角的正弦值为
;
(3)∵△A1C1B在底面ABCD中的射影为△ACB
∴面A1C1B与底面ABCD所成二面角的平面角的余弦值为
=
∴面A1C1B与底面ABCD所成二面角的平面角的正弦值
.
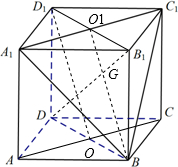
∵D1O1=BO,D1O1∥BO,∴四边形D1OBO1是平行四边形,
∴D1O∥O1B
∵D1O?平面A1C1B,O1B?平面A1C1B,
∴D1O∥面A1C1B;
∴BD上存在中点E,使D1E∥面A1C1B;
(2)连接B1D,则B1D⊥面A1C1B,设垂足为G,则∠GBB1为直线BB1和面A1C1B所成角
∵B1G=
| 1 |
| 3 |
| ||
| 3 |
∴直线BB1和面A1C1B所成角的正弦值为
| ||
| 3 |
(3)∵△A1C1B在底面ABCD中的射影为△ACB
∴面A1C1B与底面ABCD所成二面角的平面角的余弦值为
| S△ACB |
| SABCD |
| 1 |
| 2 |
∴面A1C1B与底面ABCD所成二面角的平面角的正弦值
| ||
| 2 |


练习册系列答案
相关题目