题目内容
已知△ABC的三个内角∠A,∠B,∠C所对的边分别为a,b,c,且
=-
,则角A的大小为______.
| cosA |
| cosB |
| a |
| b+2c |
∵
=-
,∴根据正弦定理,得
=-
,
即sinBcosA+2sinCcosA=-cosBcosA,
整理得-2sinCcosA=sinBcosA+cosBcosA=sin(A+B),
∵在△ABC中,sin(A+B)=sin(π-C)=sinC>0,
∴-2sinCcosA=sinC,约去sinC得cosA=-
.
又∵A∈(0,π),∴A=
.
故答案为:
| cosA |
| cosB |
| a |
| b+2c |
| cosA |
| cosB |
| sinA |
| sinB+2sinC |
即sinBcosA+2sinCcosA=-cosBcosA,
整理得-2sinCcosA=sinBcosA+cosBcosA=sin(A+B),
∵在△ABC中,sin(A+B)=sin(π-C)=sinC>0,
∴-2sinCcosA=sinC,约去sinC得cosA=-
| 1 |
| 2 |
又∵A∈(0,π),∴A=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
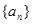 ,满足
,满足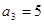 且
且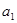 ,
,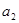 ,
,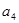 成等比数列.
成等比数列.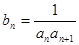 ,求数列
,求数列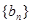 前
前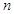 项的和为
项的和为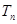 .
.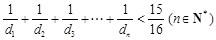 .
.