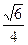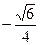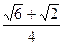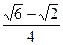题目内容
在120°的二面角α-l-β内有一点P,P在平面α、β内的射影A、B分别落在半平面αβ内,且PA=3,PB=4,则P到l的距离为______.
∵在120°的二面角α-l-β内有一点P,
P在平面α、β内的射影A、B分别落在半平面αβ内,
∴∠APB=60°
又∵PA=3,PB=4,
∴AB=
=
,
而P到l的距离即为△PAB的外接圆直径,
由正弦定理得2R=
=
=
,
故答案为:
.
P在平面α、β内的射影A、B分别落在半平面αβ内,
∴∠APB=60°
又∵PA=3,PB=4,
∴AB=
| PA2+PB2-2PA•PB•cos∠APB |
| 13 |
而P到l的距离即为△PAB的外接圆直径,
由正弦定理得2R=
| AB |
| sin∠APB |
| ||||
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
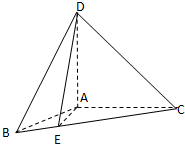
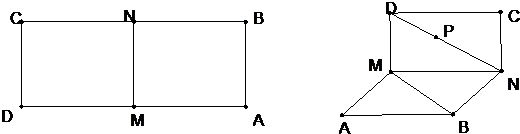
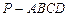 中,底面
中,底面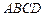 是一直角梯形,
是一直角梯形,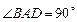 ,
,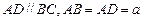 ,
,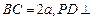 底面
底面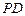 上是否存在一点
上是否存在一点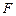 ,使得
,使得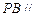 平面
平面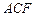 ,若存在,求出
,若存在,求出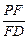 的值;
的值;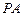 与
与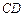 所成的角为
所成的角为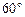 ,求二面角
,求二面角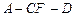 的余弦值.
的余弦值.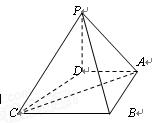
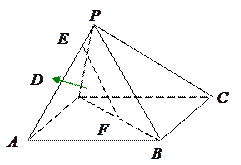
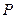 是平行四边形
是平行四边形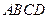 所在平面外的一点,
所在平面外的一点,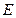 、
、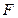 分别是
分别是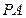 、
、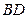 上的点且
上的点且 ,求证:
,求证: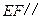 平面
平面 .
.
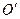 为其圆心)上,且点A、C、D、
为其圆心)上,且点A、C、D、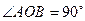 ,则异面直线AB与CD所成角的余弦值为 ( )
,则异面直线AB与CD所成角的余弦值为 ( )