题目内容
【题目】设f(x)=ln(x+1)+ ![]() +ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=
+ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0<x<2时,f(x)< ![]() .
.
【答案】
(1)
解:由y=f(x)过(0,0),∴f(0)=0,∴b=﹣1
∵曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
∴y′|x=0= ![]()
∴a=0;
(2)
证明:由(1)知f(x)=ln(x+1)+ ![]() -1
-1
由均值不等式,当x>0时, ![]() ,∴
,∴ ![]() ①
①
令k(x)=ln(x+1)﹣x,则k(0)=0,k′(x)= ![]() ,∴k(x)<0
,∴k(x)<0
∴ln(x+1)<x,②
由①②得,当x>0时,f(x)< ![]() x
x
记h(x)=(x+6)f(x)﹣9x,则当0<x<2时,h′(x)=f(x)+(x+6)f′(x)﹣9
< ![]() <
< ![]()
= ![]()
∴h(x)在(0,2)内单调递减,又h(0)=0,∴h(x)<0
∴当0<x<2时,f(x)< ![]()
【解析】(1)由y=f(x)过(0,0),可求b的值,根据曲线y=f(x)与直线y= ![]() x在(0,0)点相切,利用导函数,可求a的值;(2)由(1)知f(x)=ln(x+1)+
x在(0,0)点相切,利用导函数,可求a的值;(2)由(1)知f(x)=ln(x+1)+ ![]() -1,由均值不等式,可得
-1,由均值不等式,可得 ![]() ,构造函数k(x)=ln(x+1)﹣x,可得ln(x+1)<x,从而当x>0时,f(x)<
,构造函数k(x)=ln(x+1)﹣x,可得ln(x+1)<x,从而当x>0时,f(x)< ![]() x,记h(x)=(x+6)f(x)﹣9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证
x,记h(x)=(x+6)f(x)﹣9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).

【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在![]() 内,已知该产品的成本是
内,已知该产品的成本是![]() 元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
参考数据:![]()
参考公式: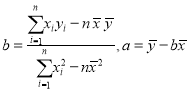
【题目】某种机器零件转速在符合要求的范围内使用时间随机器运转速度的变化而变化,某检测员随机收集了20个机器零件的使用时间与转速的数据,列表如下:
机器转速(转/分) | 189 | 193 | 190 | 185 | 183 | 202 | 187 | 203 | 192 | 201 |
零件使用时间(月) | 43 | 33 | 39 | 37 | 38 | 37 | 38 | 35 | 38 | 35 |
机器转速(转/分) | 193 | 197 | 191 | 186 | 191 | 188 | 185 | 204 | 201 | 189 |
零件使用时间(月) | 37 | 40 | 41 | 37 | 35 | 37 | 42 | 36 | 34 | 40 |
(Ⅰ)若“转速大于200转/分”为“高速”,“转速不大于200转/分”为“非高速”,“使用时间大于36个月”的为“长寿命”,“使用时间不大于36个月”的为“非长寿命”,请根据上表数据完成下面的![]() 列联表:
列联表:
高速 | 非高速 | 合计 | |
长寿命 | |||
非长寿命 | |||
合计 |
(Ⅱ)根据(Ⅰ)中的![]() 列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |


