题目内容
8. 如图,圆锥的底面直径AB=2,母线长VA=3,点C在母线长VB上,且VC=1,有一只蚂蚁沿圆锥的侧面从点A到点C,则这只蚂蚁爬行的最短距离是( )
如图,圆锥的底面直径AB=2,母线长VA=3,点C在母线长VB上,且VC=1,有一只蚂蚁沿圆锥的侧面从点A到点C,则这只蚂蚁爬行的最短距离是( )| A. | $\sqrt{13}$ | B. | $\sqrt{7}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
分析 要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答 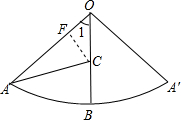 解:由题意知,底面圆的直径为2,故底面周长等于2π,
解:由题意知,底面圆的直径为2,故底面周长等于2π,
设圆锥的侧面展开后的扇形圆心角为α,
根据底面周长等于展开后扇形的弧长得,2π=3α,
解得:α=$\frac{2π}{3}$,
∴∠AOA′=$\frac{2π}{3}$,
则∠1=$\frac{π}{3}$,
过C作CF⊥OA,
∵C为OB的三等分点,BO=3,
∴OC=1,
∵∠1=60°,
∴∠OCF=30°,
∴FO=$\frac{1}{2}$,
∴CF2=CO2-OF2=$\frac{3}{4}$,
∵AO=3,FO=$\frac{1}{2}$,
∴AF=$\frac{5}{2}$,
在Rt△AFC中,利用勾股定理得:AC2=AF2+FC2=7,
则AC=$\sqrt{7}$.
故选:B.
点评 考查了平面展开-最短路径问题,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
相关题目
16.在△ABC中,AB=3,AC=4,BC=5.若I为△ABC的内心,则$\overrightarrow{CI}$•$\overrightarrow{CB}$的值为( )
| A. | 6 | B. | 10 | C. | 12 | D. | 15 |
17.已知点M(1,1),N(4,-3),则与向量$\overrightarrow{MN}$共线的单位向量为( )
| A. | ($\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{3}{5}$,$\frac{4}{5}$) | C. | ($\frac{3}{5}$,-$\frac{4}{5}$)或(-$\frac{3}{5}$,$\frac{4}{5}$) | D. | ($\frac{4}{5}$,-$\frac{3}{5}$)或(-$\frac{4}{5}$,$\frac{3}{5}$) |