题目内容
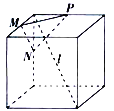
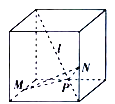
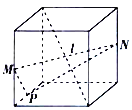
【题目】如图,已知点![]() 是椭圆
是椭圆![]() 上的任意一点,直线
上的任意一点,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率都存在.
的斜率都存在.

(1)若直线![]() 过原点,求证:
过原点,求证:![]() 为定值;
为定值;
(2)若直线![]() 不过原点,且
不过原点,且![]() ,试探究
,试探究![]() 是否为定值.
是否为定值.
【答案】(1)见解析(2)![]() ,详见解析
,详见解析
【解析】
(1)设![]() ,
,![]() ,由椭圆对称性得
,由椭圆对称性得![]() ,把点
,把点![]() ,
,![]() 的坐标都代入椭圆得到两个方程,再相减,得到两直线斜率乘积的表达式;
的坐标都代入椭圆得到两个方程,再相减,得到两直线斜率乘积的表达式;
(2)设![]() ,
,![]() ,
,![]() ,则
,则![]() ,由
,由![]() 得:
得:![]() ,进而得到直线
,进而得到直线![]() 的方程,再与椭圆方程联立,利用韦达定理得到坐标之间的关系,最后整体代入消元,得到
的方程,再与椭圆方程联立,利用韦达定理得到坐标之间的关系,最后整体代入消元,得到![]() 为定值.
为定值.
(1)当![]() 过原点时,设
过原点时,设![]() ,
,![]() ,由椭圆对称性得
,由椭圆对称性得![]() ,
,
则![]() .
.
∵![]() ,
,![]() 都在椭圆
都在椭圆![]() 上,∴
上,∴![]() ,
,![]() ,
,
两式相减得: 故 (2)设 ∴ 联立方程组 整理得 ∵ 上式可化为 ∴ ∴ ∴ ∴![]() ,即
,即![]() .
.![]() .
. ![]() ,
,![]() ,
,![]() ,则
,则![]() ,∵
,∵![]() ,
,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() (
(![]() ),
), 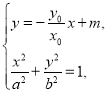 消去
消去![]() ,
,![]() .
.![]() 在椭圆上,∴
在椭圆上,∴![]() ,
,![]() .
.![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ;
;![]()
![]() .
.![]() (定值).
(定值).

练习册系列答案
相关题目