题目内容
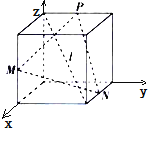
【题目】如图所示,在四个正方体中,![]() 是正方体的一条体对角线,点
是正方体的一条体对角线,点![]() 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出![]() 平面
平面![]() 的图形为( )
的图形为( )
A.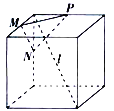 B.
B.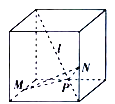
C. D.
D.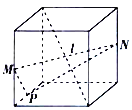
【答案】AD
【解析】
利用线面垂直的判定定理证明AD满足,结合空间向量在BC中证明直线l与平面内的某条直线不垂直,即可得线面不可能垂直.
如图所示,正方体![]() .连接
.连接![]() ,
,![]() 分别为其所在棱的中点,
分别为其所在棱的中点,![]() .
.
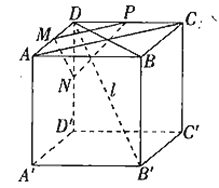
∵四边形![]() 为正方形,
为正方形,
![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() ,
,![]() ,同理,可证
,同理,可证![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,即l垂直平面
,即l垂直平面![]() ,故A正确.
,故A正确.
在D中,由A中证明同理可证![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() .故D正确.
.故D正确.
假设直线与平面垂直,则这条直线垂直于面内任何一条直线.
对于B选项建立直角坐标系如图:设棱长为2,

![]() ,直线l所在体对角线两个顶点坐标
,直线l所在体对角线两个顶点坐标![]() ,
,
所以其方向向量![]() ,
,
![]() ,所以直线不可能垂直于平面
,所以直线不可能垂直于平面![]() .
.
同理可在C中建立相同直角坐标系,![]() ,
,
![]() ,所以直线不可能垂直于平面
,所以直线不可能垂直于平面![]() .
.
故选:AD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】2018 年1月16日,由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓,某知名网站财经频道为了解公众对这些年度人物是否了解,利用网络平台进行了调查,并从参与调查者中随机选出![]() 人,把这
人,把这![]() 人分为
人分为![]() 两类(
两类(![]() 类表示对这些年度人物比较了解,
类表示对这些年度人物比较了解,![]() 类表示对这些年度人物不太了解),并制成如下表格:
类表示对这些年度人物不太了解),并制成如下表格:
年龄段 |
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
(1)若按照年龄段进行分层抽样,从这![]() 人中选出
人中选出![]() 人进行访谈,并从这
人进行访谈,并从这![]() 人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在
人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间,另一名幸运者的年龄在
岁之间,另一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间的概率;(注:从
岁之间的概率;(注:从![]() 人中随机选出
人中随机选出![]() 人,共有
人,共有![]() 种不同选法)
种不同选法)
(2)如果把年龄在![]() 岁~
岁~![]() 岁之间的人称为青少年,年龄在
岁之间的人称为青少年,年龄在![]() 岁~
岁~![]() 岁之间的人称为中老年,则能否在犯错误的概率不超过
岁之间的人称为中老年,则能否在犯错误的概率不超过![]() 的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()

