题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是椭圆
是椭圆![]() 的上焦点.问:是否存在直线
的上焦点.问:是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]()
(2)存在直线![]() :
:![]() 或
或![]() 合题意.
合题意.
【解析】
(1)由短轴长为![]() 求出b,再由离心率为
求出b,再由离心率为![]() 及
及![]() 解得:
解得:![]() ,
,![]() ,从而得解。
,从而得解。
(2)由![]() 可得:
可得:![]() 为线段
为线段![]() 的中点,设直线方程:
的中点,设直线方程:![]() ,联立直线方程与椭圆方程,表示出
,联立直线方程与椭圆方程,表示出![]() ,
,![]() ,再利用中点坐标公式列方程即可求解。
,再利用中点坐标公式列方程即可求解。
解:(1)∵![]() ,
,![]() ,且有
,且有![]() ,
,
解得![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)由题可知![]() 的斜率一定存在,设
的斜率一定存在,设![]() 为
为![]() ,设
,设![]() ,
,![]() ,
,
联立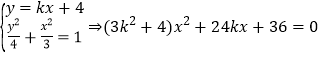
∴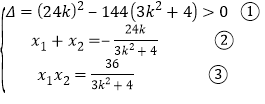
∵![]() ,∴
,∴![]() 为线段
为线段![]() 的中点,
的中点,
∴![]() ……④
……④
将④代入②解得![]() ……⑤
……⑤
将④代入③得![]() ……⑥
……⑥
将⑤代入⑥解得![]() ……⑦
……⑦
将⑦式代入①式检验成立,
∴![]() ,即存在直线
,即存在直线![]() :
:![]() 或
或![]() 合题意.
合题意.

【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |