题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)对任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() (2)函数
(2)函数![]() 取得最大值
取得最大值![]() (3)
(3)![]()
【解析】
(1)将![]() 代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
(2)![]() ,则
,则![]() ,对函数求导,判断单调性,根据单调性即可得出函数在区间
,对函数求导,判断单调性,根据单调性即可得出函数在区间![]() 上的最大值.
上的最大值.
(3)由(1)(2)得,![]() ,分情况讨论
,分情况讨论![]() 、
、![]() 时函数的单调性,从而得出实数
时函数的单调性,从而得出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时, 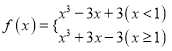 ,
,
若![]() 时,则
时,则![]() ,令
,令![]() ,解得
,解得![]() ;
;
若![]() 时,则
时,则![]() 恒成立,所以
恒成立,所以![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)若![]() ,当
,当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,解得
,解得![]() 或
或![]() .
.
列表如下:
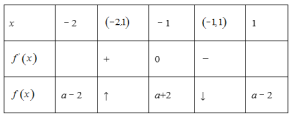
当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
(3)由(1)(2)得,![]() .
.
①当![]() 时,即
时,即![]() 时,
时,
![]() ,即
,即![]() .
.
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,
,
所以![]() ,解得
,解得![]() ,又
,又![]() ,所以
,所以![]() .
.
②当![]() 即
即![]() 时,
时,
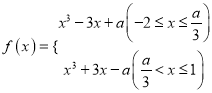
当![]() 时,
时,![]() ,即
,即![]() ,
,
与![]() 矛盾,
矛盾,
所以,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某公司统计了2010~2018年期间公司年收的增加值![]() (万元)以及相应的年增长率
(万元)以及相应的年增长率![]() ,所得数据如下所示:
,所得数据如下所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
增加值 | 1555 | 2100 | 2220 | 2740 | 3135 | 3563 | 4041 | 5494.4 | 6475 |
增长率 |
|
|
|
|
|
|
|
|
|
(1)通过散点图可知,可用线性回归模型拟合2010~2014年![]() 与
与![]() 的关系;
的关系;
①求2010~2014年这5年期间公司年利润的增加值的平均数![]() ;
;
②求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)从哪年开始连续三年公司利润增加值的方差最大?(不需要说明理由)
附:参考公式:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为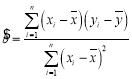 ,
,![]() .
.