题目内容
【题目】在直角坐标系
中，曲线
与
轴交于
，
两点，点
的坐标为
，当
变化时，解答下列问题：
（
）能否出现
的情况?说明理由．
（
）证明过，，三点的圆在
轴上截得的弦长为定值．
【答案】（
）见解析．（
）见解析．
【解析】试题分析：（1）设设
，
，并用根与系数关系表示出
，
，计算
的值，根据其不为0可知不能出现
的情况；
（2）设圆心E的坐标，并分别表示出其横、纵坐标的值，根据圆E的方程可得过A、B、C 三点的圆在y轴上截得的弦长.
试题解析：（）设，，则
，
是方程
的两根，
所以，，
则
，
所以不能出现的情况．
（）过
，
，
三点的圆的圆心必在线段
的垂直平分线上，
设圆心
，则
，由
得
，化简得
，
所以圆
的方程为
，
令
，得
，
，
所以过，，三点的圆在
轴上截得的弦长为
，
所以过，，三点的圆在轴上截得的弦长为定值．
练习册系列答案
相关题目
【题目】某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20，30） | 30 | 18 |
[30，40） | 36 | 24 |
[40，50） | 12 | 9 |
[50，60] | 4 | 3 |
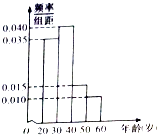
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
