题目内容
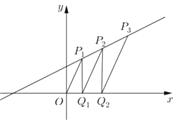
【题目】如图,O坐标原点,从直线y![]() x+1上的一点
x+1上的一点![]() 作x轴的垂线,垂足记为Q1,过Q1作OP1的平行线,交直线y
作x轴的垂线,垂足记为Q1,过Q1作OP1的平行线,交直线y![]() x+1于点
x+1于点![]() ,再从P2作x轴的垂线,垂足记为Q2,依次重复上述过程得到一系列点:P1,Q1,P2,Q2,…,Pn,Qn,记Pk点的坐标为
,再从P2作x轴的垂线,垂足记为Q2,依次重复上述过程得到一系列点:P1,Q1,P2,Q2,…,Pn,Qn,记Pk点的坐标为![]() ,k=1,2,3,…,n,现已知x1=2.
,k=1,2,3,…,n,现已知x1=2.
(1)求Q2、Q3的坐标;
(2)试求xk(1≤k≤n)的通项公式;
(3)点Pn、Pn+1之间的距离记为|PnPn+1|(n∈N*),是否存在最小的正实数t,使得![]() t对一切的自然数n恒成立?若存在,求t的值,若不存在,请说明理由
t对一切的自然数n恒成立?若存在,求t的值,若不存在,请说明理由
【答案】(1) Q2(6,0),Q3(14,0);(2)![]() ,1≤k≤n; (3)存在,
,1≤k≤n; (3)存在,![]() .
.
【解析】
(1)首先根据OP1∥P2Q1,计算出Q2的坐标,再根据OP1∥P3Q2即可计算出Q3的坐标。
(2)由Pk(xk,![]() xk+1),Qk﹣1(xk﹣1,0),OP1∥PkQk﹣1,可得
xk+1),Qk﹣1(xk﹣1,0),OP1∥PkQk﹣1,可得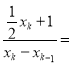 1,化为xk=2xk﹣1+2,利用配凑法即可计算出通项式,
1,化为xk=2xk﹣1+2,利用配凑法即可计算出通项式,
(3)利用|PnPn+1|![]() |xn+1﹣xn|
|xn+1﹣xn|![]() |2n+2﹣2n+1|
|2n+2﹣2n+1|![]() 2n,可得
2n,可得![]() (
(![]() )
)![]()
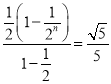 (1
(1![]() )
)![]() 。
。
(1)x1=2,即有P1(2,2),![]() ,Q1(2,0),P2(x2,
,Q1(2,0),P2(x2,![]() x2+1),OP1∥P2Q1,
x2+1),OP1∥P2Q1,
可得![]()
 1,解得x2=6,则Q2(6,0),由P2(6,4),P3(x3,
1,解得x2=6,则Q2(6,0),由P2(6,4),P3(x3,![]() x3+1),
x3+1),
OP1∥P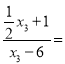 1,解得x3=14,Q3(14,0);
1,解得x3=14,Q3(14,0);
(2)由Pk(xk,![]() xk+1),Qk﹣1(xk﹣1,0),
xk+1),Qk﹣1(xk﹣1,0),
OP1∥PkQk﹣1,可得
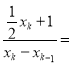 1,化为xk=2xk﹣1+2,
1,化为xk=2xk﹣1+2,
即为xk+2=2(xk﹣1+2),
可得数列{xk+2}为首项是4,公比为2的等比数列,
则xk+2=42k﹣1,
可得![]() ,1≤k≤n;
,1≤k≤n;
(3)|PnPn+1|![]()
![]() |xn+1﹣xn|
|xn+1﹣xn|![]() |2n+2﹣2n+1|
|2n+2﹣2n+1|![]() 2n,
2n,
![]() (
(![]() )
)![]()
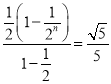 (1
(1![]() )
)![]() ,
,
假设存在最小的正实数t,使得![]() t对一切的自然数n恒成立,
t对一切的自然数n恒成立,
可得t![]() ,故存在这样的t,且t的最小值为
,故存在这样的t,且t的最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案