题目内容
7.已知命题p:?x∈R,2x<3x;命题q:?x∈R,使得log0.5x=x,则下列命题中为真命题的是( )| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
分析 对于命题p:由2x<3x,化为$(\frac{2}{3})^{x}$<1,利用指数函数的单调性解出x范围,即可判断出命题p真假;对于命题q:令f(x)=log0.5x-x,利用函数零点存在判定定理可得?x∈$(\frac{1}{2},1)$,使得f(x)=0,即可判断出真假.再利用复合命题真假的判定方法即可判断出.
解答 解:对于命题p:由2x<3x,化为$(\frac{2}{3})^{x}$<1,因此x>0,故x≤0时不成立,因此p是假命题;
对于命题q:令f(x)=log0.5x-x,∵$f(\frac{1}{2})$=1-$\frac{1}{2}$=$\frac{1}{2}$>0,f(1)=0-1=-1<0,∴?x∈$(\frac{1}{2},1)$,使得f(x)=0,
因此命题q是真命题.
∴p∧q,p∧¬q,¬p∧¬q是假命题;
∴¬p∧q是真命题.
故选:B.
点评 本题考查了函数的性质、函数零点的判定定理、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.八人分乘三辆小车,每辆小车至少载1人最多载4人,不同坐法共有( )
| A. | 770种 | B. | 1260种 | C. | 4620种 | D. | 2940种 |
17.冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示.
根据以上数据,则( )
| 杂质高 | 杂质低 | |
| 旧设备 | 37 | 121 |
| 新设备 | 22 | 202 |
| A. | 含杂质的高低与设备改造有关 | B. | 含杂质的高低与设备改造无关 | ||
| C. | 设备是否改造决定含杂质的高低 | D. | 以上答案都不对 |
12.已知sinθ=$\frac{3}{5}$,且θ∈(0,$\frac{π}{2}}$),则$\frac{sin2θ}{{{{cos}^2}θ}}$的值等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{3}{4}$ |
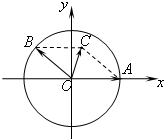 如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).