题目内容
若方程ax2＋ay2－4(a－1)x＋4y＝0表示圆，求实数a的取值范围，并求出半径最小的圆的方程．
a≠0，半径最小的圆的方程为(x－1)2＋(y＋1)2＝2.
∵方程ax2＋ay2－4(a－1)x＋4y＝0表示圆，∴a≠0.
∴方程ax2＋ay2－4(a－1)x＋4y＝0可以写成x2＋y2－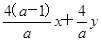
＝0.
∵D2＋E2－4F＝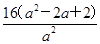
>0恒成立，
∴a≠0时，方程ax2＋ay2－4(a－1)x＋4y＝0表示圆．设圆的半径为r，则
r2＝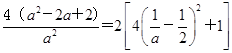
，
∴当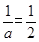
即，a＝2时，圆的半径最小，半径最小的圆的方程为(x－1)2＋(y＋1)2＝2
∴方程ax2＋ay2－4(a－1)x＋4y＝0可以写成x2＋y2－
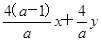＝0.∵D2＋E2－4F＝
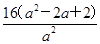>0恒成立，∴a≠0时，方程ax2＋ay2－4(a－1)x＋4y＝0表示圆．设圆的半径为r，则
r2＝
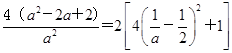，∴当
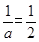即，a＝2时，圆的半径最小，半径最小的圆的方程为(x－1)2＋(y＋1)2＝2
练习册系列答案
相关题目
(t∈R，t≠0)为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为原点．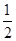
)2＋(y－
三个顶点的坐标分别是
，则该三角形外接圆方程是 .
在圆
的内部，则
的取值范围是（ ）
