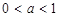题目内容
已知圆 ,
,
(Ⅰ)若过定点( )的直线
)的直线 与圆
与圆 相切,求直线
相切,求直线 的方程;
的方程;
(Ⅱ)若过定点( )且倾斜角为
)且倾斜角为 的直线
的直线 与圆
与圆 相交于
相交于 两点,求线段
两点,求线段 的中点
的中点 的坐标;
的坐标;
(Ⅲ) 问是否存在斜率为 的直线
的直线 ,使
,使 被圆
被圆 截得的弦为
截得的弦为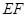 ,且以
,且以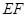 为直径的圆经过原点?若存在,请写出求直线
为直径的圆经过原点?若存在,请写出求直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
 ,
,(Ⅰ)若过定点(
 )的直线
)的直线 与圆
与圆 相切,求直线
相切,求直线 的方程;
的方程;(Ⅱ)若过定点(
 )且倾斜角为
)且倾斜角为 的直线
的直线 与圆
与圆 相交于
相交于 两点,求线段
两点,求线段 的中点
的中点 的坐标;
的坐标;(Ⅲ) 问是否存在斜率为
 的直线
的直线 ,使
,使 被圆
被圆 截得的弦为
截得的弦为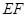 ,且以
,且以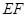 为直径的圆经过原点?若存在,请写出求直线
为直径的圆经过原点?若存在,请写出求直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。(Ⅰ)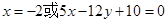 ,(Ⅱ)
,(Ⅱ)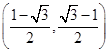 (Ⅲ)
(Ⅲ)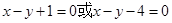
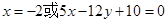 ,(Ⅱ)
,(Ⅱ)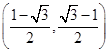 (Ⅲ)
(Ⅲ)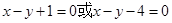
试题分析:(Ⅰ)求过定点直线方程,要注意斜率不存在情况是否满足题意,本题可分类讨论,也可从设法上考虑斜率不存在,即设直线
 的方程为:
的方程为: ,再利用圆心到直线距离等于半径即可求出直线方程,(Ⅱ)求圆中弦中点,一可利用几何条件,即圆心与弦中点连线与直线垂直,从而弦中点就为直线
,再利用圆心到直线距离等于半径即可求出直线方程,(Ⅱ)求圆中弦中点,一可利用几何条件,即圆心与弦中点连线与直线垂直,从而弦中点就为直线 :
: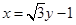 与连线
与连线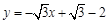 的交点,二可利用韦达定理,根据中点坐标公式求解,(Ⅲ)以
的交点,二可利用韦达定理,根据中点坐标公式求解,(Ⅲ)以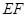 为直径的圆经过原点,这一条件如何用,是解题的关键 一是利用向量垂直,二是利用圆系方程
为直径的圆经过原点,这一条件如何用,是解题的关键 一是利用向量垂直,二是利用圆系方程 试题解析:(Ⅰ)根据题意,设直线
 的方程为:
的方程为:
联立直线与圆的方程并整理得:
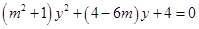 2分
2分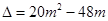 所以
所以
从而,直线
 的方程为:
的方程为: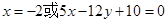 4分
4分(Ⅱ)根据题意,设直线
 的方程为:
的方程为: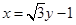
代入圆
 方程得:
方程得: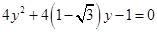 ,显然
,显然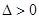 , 6分
, 6分设
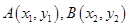 则
则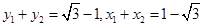
所以点
 的坐标为
的坐标为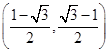 8分
8分(Ⅲ)假设存在这样的直线
 :
: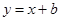
联立圆的方程并整理得:
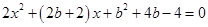
当
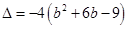
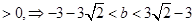 9分
9分设
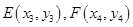 则
则
所以
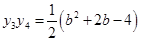 10分
10分因为以
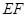 为直径的圆经过原点,所以
为直径的圆经过原点,所以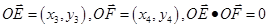
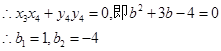 均满足
均满足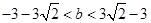 。
。所以直线
 的方程为:
的方程为: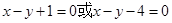 。 13分
。 13分(Ⅲ)法二:可以设圆系方程
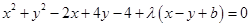
则圆心坐标
 ,圆心在直线
,圆心在直线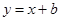 上,且该圆过原点。易得b的值。
上,且该圆过原点。易得b的值。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
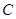 经过坐标原点
经过坐标原点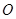 和点
和点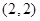 ,且圆心在
,且圆心在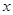 轴上.
轴上.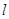 经过点
经过点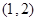 ,且
,且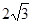 ,求直线
,求直线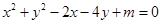 .(14分)
.(14分)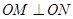 (O为坐标原点),求m的值;
(O为坐标原点),求m的值;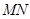 为直径的圆的方程.
为直径的圆的方程.
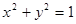 上的点到点
上的点到点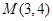 的距离的最小值是( )
的距离的最小值是( )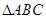 三个顶点的坐标分别是
三个顶点的坐标分别是 ,则该三角形外接圆方程是 .
,则该三角形外接圆方程是 .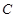 :
: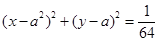
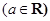 ,则下列命题:①圆
,则下列命题:①圆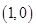 的最短距离的最小值为
的最短距离的最小值为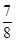 ;②圆
;②圆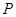 到点
到点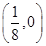 的距离与到直线
的距离与到直线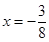 的距离相等;③已知
的距离相等;③已知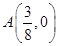 ,在圆
,在圆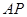 为直径的圆与直线
为直径的圆与直线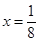 相切.真命题的个数为
相切.真命题的个数为

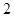

 在圆
在圆 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )