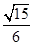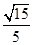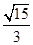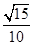题目内容
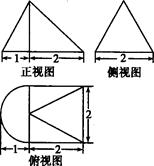
一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )
A.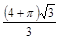 | B.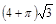 | C. | D.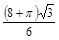 |
D
解析试题分析:由已知中的三视图,我们可以判断出该几何体的形状,及关键数据,代入棱锥体积公式,即可求出答案.由于该几何体有一个半圆锥和一个四棱维组合而成,
其中半圆锥的底面半径为1,四棱锥的底面是一个边长为2为正方形,他们的高均为 ,则v=
,则v= 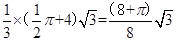 , 答案选D
, 答案选D
考点:本题主要考查知识点是由三视图求体积。
点评:解决该试题的关键是其中根据已知中的三视图判断出几何体的形状。结合棱锥的体积公式求解运算得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
正方体的内切球,与各棱相切的球,外接球的体积之比为( )
| A.1:2:3 | B.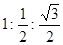 | C.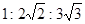 | D.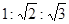 |
正方体的棱长为 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
A. | B.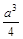 | C. | D. |
把正方形 沿对角线
沿对角线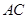 折起,当以
折起,当以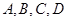 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线 和平面
和平面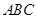 所成的角的大小为( )
所成的角的大小为( )
A.90 | B.30 | C.60 | D.45 |
某几何体的三视图如右图所示,则其侧面积为 
A. | B. | C. | D. |

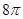

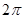
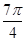
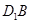 所成角的余弦值为()
所成角的余弦值为()