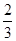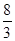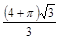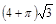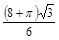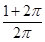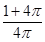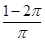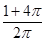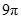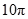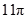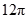题目内容
正方体的棱长为
，由它的互不相邻的四个顶点连线所构成的四面体的体积是（ ）
A． | B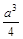． | C． | D． |
B.
解析试题分析：此几何体是棱长为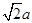
的正四面体，所以其体积为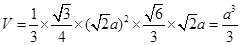
考点：正方体的性质，正四面体的性质及体积.
点评：所求四面体的各条棱是正方体的面对角线，所以其棱长为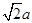,正四面体的高等于棱长的
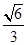倍，记住这些结论有利用快速解题.
练习册系列答案
相关题目
球的表面积与它的内接正方体的表面积之比是（ ）
A． | B． | C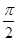． | D． |
如图所示的直观图，其原来平面图形的面积是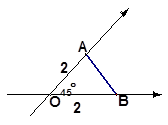
| A．4 |
B．4 |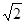
| C．2 |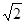
| D．8 |
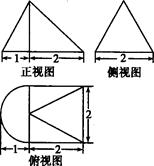
某三棱锥的侧视图和俯视图如图所示，则该三棱锥的体积为 ( )
A．4 | B．8 | C．12 | D．24 |