题目内容
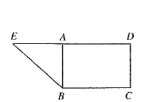
【题目】已知椭圆![]() 的左焦点为F,上顶点为A,直线AF与直线
的左焦点为F,上顶点为A,直线AF与直线![]() 垂直,垂足为B,且点A是线段BF的中点.
垂直,垂足为B,且点A是线段BF的中点.
(I)求椭圆C的方程;
(II)若M,N分别为椭圆C的左,右顶点,P是椭圆C上位于第一象限的一点,直线MP与直线![]() 交于点Q,且
交于点Q,且![]() ,求点P的坐标.
,求点P的坐标.
【答案】(I)![]() .
.
(II)![]()
【解析】
(I)写出![]() 坐标,利用直线
坐标,利用直线![]() 与直线
与直线![]() 垂直,得到
垂直,得到![]() .求出
.求出![]() 点的坐标代入
点的坐标代入![]() ,可得到
,可得到![]() 的一个关系式,由此求得
的一个关系式,由此求得![]() 和
和![]() 的值,进而求得椭圆方程.(II)设出
的值,进而求得椭圆方程.(II)设出![]() 点的坐标,由此写出直线
点的坐标,由此写出直线![]() 的方程,从而求得
的方程,从而求得![]() 点的坐标,代入
点的坐标,代入![]() ,化简可求得
,化简可求得![]() 点的坐标.
点的坐标.
(I)∵椭圆的左焦点![]() ,上顶点
,上顶点![]() ,直线AF与直线
,直线AF与直线![]() 垂直
垂直
∴直线AF的斜率![]() ,即
,即![]() ①
①
又点A是线段BF的中点
∴点![]() 的坐标为
的坐标为![]()
又点![]() 在直线
在直线![]() 上
上
∴![]() ②
②
∴由①②得:![]()
∴![]()
∴椭圆![]() 的方程为
的方程为![]() .
.
(II)设![]()
由(I)易得顶点M、N的坐标为![]()
∴直线MP的方程是:![]()
由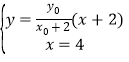 得:
得:![]()
又点P在椭圆上,故![]()
∴![]()
∴![]()
∴![]() 或
或![]() (舍)
(舍)
∴![]()
∴点P的坐标为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目