题目内容
【题目】某房地产开发商有一块如图(1)所示的四边形空地ABCD,经测量,边界CB与CD的长都为2km,所形成的角∠![]() .
.
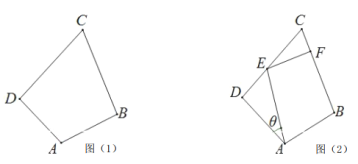
(I)如果边界AD与AB所形成的角![]() ,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
(II)当边界AD与CD垂直,AB与BC垂直时,为后期开发方便,拟在这块空地上先建两条内部道路AE,EF,如图(2)所示,点E在边界CD上,且道路EF与边界BC互相垂直,垂足为F,为节约成本,欲将道路AE,EF分别建成水泥路、砂石路,每1km的建设费用分别为![]() 、a元(a为常数);若设
、a元(a为常数);若设![]() ,试用
,试用![]() 表示道路AE,EF建设的总费用
表示道路AE,EF建设的总费用![]() (单位:元),并求出总费用
(单位:元),并求出总费用![]() 的最小值.
的最小值.
【答案】(I)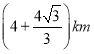 (II)
(II)![]() ;最小值为
;最小值为![]() 元.
元.
【解析】
(I)由题意结合余弦定理得![]() ,利用基本不等式即可得解;
,利用基本不等式即可得解;
(II)由正弦定理得![]() ,则
,则![]() ,由题意可得
,由题意可得![]() ,
,![]() ,令
,令![]() ,
,![]() ,求导得到
,求导得到![]() 最小值即可得解.
最小值即可得解.
(I)连结BD,易知![]() 为等边三角形,则
为等边三角形,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理得:![]()
即![]()
由基本不等式得:![]()
则![]() (当且仅当
(当且仅当![]() 时“=”成立).
时“=”成立).
则![]() .
.
答:所用板材长度的最大值为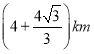 .
.
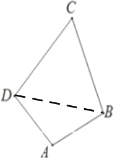
(Ⅱ)因为AD与CD垂直,AB与BC垂直,
则ABCD四点共圆,且AC为直径,记直径为2R.
在ABCD中,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由正弦定理得:![]() ,
,
在![]() 和
和![]() 中,则
中,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
又![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
则![]() ,
,
所以总费用![]() .
.
记![]() ,
,![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() .
.
答.铺设的总费用的最小值为![]() 元.
元.

【题目】某种新型嫁接巨丰葡萄,在新疆地区种植一般亩产不低于5千斤,产量高的达到上万斤.受嫁接年限的影响,其产量一般逐年衰减,若在新疆地区平均亩产量低于5千斤,则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y(单位:千斤)的数据表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归直线方程,预计哪一年开始从新嫁接.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: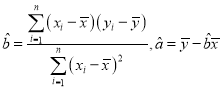 .
.