题目内容
【题目】如图，在直角梯形
中，
，
，
是
上一点，
，现沿
将
折起到
的位置，并使
平面
，点
在
边上，且满足
.
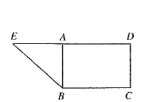
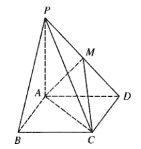
（1）证明：
平面
；
（2）若
，
，
，求二面角
的大小.
【答案】（1）详见解析；（2）
.
【解析】
（1）连接
交
于点
，由矩形的性质及三角形的中位线定理得
，再根据直线与平面平行的判定定理即可证明；（2）通过建立空间直角坐标系，利用平面的法向量即可求出二面角
的大小.
解：（1）连接交于点，连接
，
由已知可得四边形
是矩形，
为的中点，
又
，
为
的中点，
，
平面
，
平面，
平面.
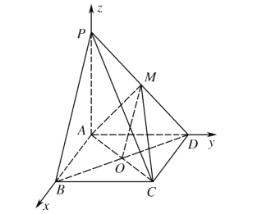
（2）由（1）及
平面可知
两两相互垂直，故以
为原点，以所在直线分别为
轴、
轴、
轴建立空间直角坐标系，
则
，
，
，
，
，
易知平面
的一个法向量为
，
，
，
设平面的法向量为
，
则由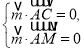
得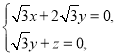
令
，解得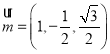
.
，
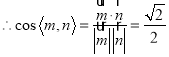由图可知二面角为锐二面角，
二面角的大小为.
练习册系列答案
相关题目
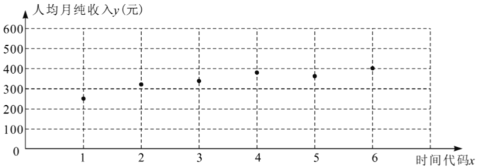
【题目】某种新型嫁接巨丰葡萄，在新疆地区种植一般亩产不低于5千斤，产量高的达到上万斤.受嫁接年限的影响，其产量一般逐年衰减，若在新疆地区平均亩产量低于5千斤，则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y（单位：千斤）的数据表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
（1）求y关于x的线性回归方程；
（2）利用（1）中的回归直线方程，预计哪一年开始从新嫁接.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：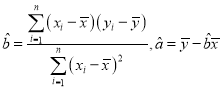
.
