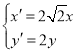Question

【题目】已知抛物线Γ：y2＝2px（p＞0）的焦点为F，P是抛物线Γ上一点，且在第一象限，满足（2，2）

（1）求抛物线Γ的方程；

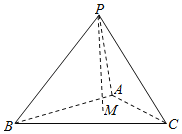
（2）已知经过点A（3，﹣2）的直线交抛物线Γ于M，N两点，经过定点B（3，﹣6）和M的直线与抛物线Γ交于另一点L，问直线NL是否恒过定点，如果过定点，求出该定点，否则说明理由．

Answer 1

【答案】（1）y2＝4x；；（2）直线NL恒过定点（﹣3，0），理由见解析.

【解析】

（1）根据抛物线的方程，求得焦点F（，0），利用（2，2），表示点P的坐标，再代入抛物线方程求解.

（2）设M（x0，y0），N（x1，y1），L（x2，y2），表示出MN的方程y和ML的方程y，因为A（3，﹣2），B（3，﹣6）在这两条直线上，分别代入两直线的方程可得y1y2＝12，然后表示直线NL的方程为：y﹣y1（x），代入化简求解.

（1）由抛物线的方程可得焦点F（，0），满足（2，2）的P的坐标为（2，2），P在抛物线上，

所以（2）2＝2p（2），即p2+4p﹣12＝0，p＞0，解得p＝2，所以抛物线的方程为：y2＝4x；

（2）设M（x0，y0），N（x1，y1），L（x2，y2），则y12＝4x1，y22＝4x2，

直线MN的斜率kMN，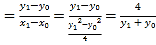

则直线MN的方程为：y﹣y0（x），

即y①，

同理可得直线ML的方程整理可得y②，

将A（3，﹣2），B（3，﹣6）分别代入①，②的方程

可得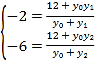，消y0可得y1y2＝12，

易知直线kNL，则直线NL的方程为：y﹣y1（x），

即yx，故yx，

所以y（x+3），

因此直线NL恒过定点（﹣3，0）．