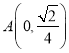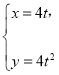题目内容
【题目】已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() ,正整数组
,正整数组![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若数组![]() 中的三个数构成公差大于
中的三个数构成公差大于![]() 的等差数列,且
的等差数列,且![]() ,求
,求![]() 的最大值.
的最大值.
(3)若![]() ,试写出满足条件的一个数组
,试写出满足条件的一个数组![]() 和对应的通项公式
和对应的通项公式![]() .(注:本小问不必写出解答过程)
.(注:本小问不必写出解答过程)
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() ,
,![]() .
.
【解析】
试题(1)由条件,知![]() 即
即 所以
所以![]() .因为
.因为![]() ,所以
,所以![]() . (2)由
. (2)由![]()
![]() ,即
,即![]() ,所以
,所以![]() ,
,
同理可得,![]() .因为
.因为![]() 成等差数列,所以
成等差数列,所以![]() .
.
记![]() ,则有
,则有![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() ,即
,即![]() .所以
.所以![]() .
.
记![]() ,则
,则![]() 为奇数,又公差大于1,所以
为奇数,又公差大于1,所以![]() ,所以
,所以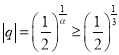 ,即
,即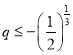 ,
,
当![]() 时,
时,![]() 取最大值为
取最大值为![]() .(3)满足题意的数组
.(3)满足题意的数组![]() , 此时通项公式为
, 此时通项公式为![]() ,
,![]() .例如:
.例如:![]() ,
,![]() .
.
试题解析:
(1)由条件,知![]() 即
即 所以
所以![]() .
.
因为![]() ,所以
,所以![]() .
.
(2)由![]()
![]() ,即
,即![]() ,所以
,所以![]() ,同理可得,
,同理可得,![]() .因为
.因为![]() 成等差数列,所以
成等差数列,所以![]() .记
.记![]() ,则有
,则有![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() ,即
,即![]() .所以
.所以![]() .记
.记![]() ,则
,则![]() 为奇数,又公差大于1,所以
为奇数,又公差大于1,所以![]() ,所以
,所以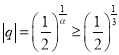 ,即
,即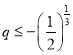 ,当
,当![]() 时,
时,![]() 取最大值为
取最大值为![]() .
.
(3)满足题意的数组![]() , 此时通项公式为
, 此时通项公式为![]() ,
,![]() .例如:
.例如:![]() ,
,![]() .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
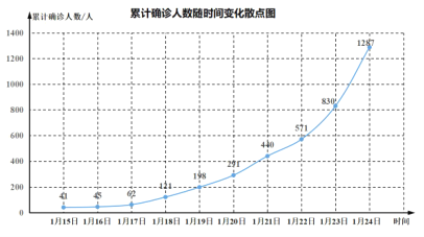
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为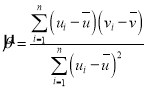 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
【题目】某种新型嫁接巨丰葡萄,在新疆地区种植一般亩产不低于5千斤,产量高的达到上万斤.受嫁接年限的影响,其产量一般逐年衰减,若在新疆地区平均亩产量低于5千斤,则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y(单位:千斤)的数据表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归直线方程,预计哪一年开始从新嫁接.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: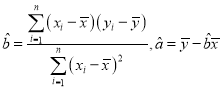 .
.