题目内容
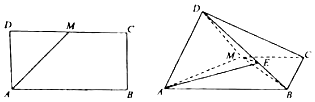
【题目】如图,M是矩形ABCD的边CD上的一点,AC与BM交于点N,BN=![]() BM.
BM.

(1)求证:M是CD的中点;
(2)若AB=2,BC=1,H是BM上异于点B的一动点,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)0
【解析】
(1) 设![]() =m
=m![]() =n
=n![]() ,再根据向量的线性运算化简
,再根据向量的线性运算化简![]() =
=![]() ,再求出
,再求出![]() =(1-n)
=(1-n)![]() +n
+n![]() ,解方程组
,解方程组 所以
所以![]() =m
=m![]() ,即M是CD的中点.(2)先利用向量的数量积和向量的线性运算求得
,即M是CD的中点.(2)先利用向量的数量积和向量的线性运算求得![]() ==-
==-![]() ,再利用二次函数求出函数的最小值.
,再利用二次函数求出函数的最小值.
(1)设![]() =m
=m![]() =n
=n![]() ,
,
由题意知![]() )
)
=![]() +m
+m![]() )=
)=![]() ,
,
又![]() +n
+n![]() +n(
+n(![]() )
)
=(1-n)![]() +n
+n![]() ,
,
∴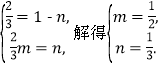
∴![]() =m
=m![]() ,即M是CD的中点.
,即M是CD的中点.
(2)∵AB=2,BC=1,M是CD的中点,
∴MB=![]() ,∠ABM=45°,
,∠ABM=45°,
∴![]() =(
=(![]() )·
)·![]() =-(
=-(![]() )·
)·![]() =-
=-![]() -|
-|![]() |2
|2
=-|![]() ||
||![]() |cos(180°-∠ABH)-|
|cos(180°-∠ABH)-|![]() |2
|2
=|![]() ||
||![]() |cos 45°-|
|cos 45°-|![]() |2
|2
=![]() |-|
|-|![]() |2=-
|2=-![]() ,
,
又0<|![]() |≤
|≤![]() ,∴当|
,∴当|![]() |=
|=![]() ,即H与M重合时,
,即H与M重合时,![]() 取得最小值,且最小值为0.
取得最小值,且最小值为0.

练习册系列答案
相关题目