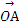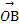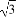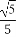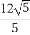题目内容
在△ABC中, AB边上的中线CO=2,若动点P满足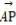 =
= sin2θ·
sin2θ·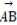 +cos2θ·
+cos2θ·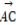 (θ∈R),则(
(θ∈R),则(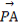 +
+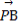 )·
)·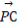 的最小值是 .
的最小值是 .
-2
【解析】【思路点拨】根据所给条件判断出点P的位置,转化为函数问题来解决.
【解析】
因为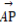 =
=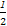 sin2θ·
sin2θ·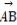 +cos2θ·
+cos2θ·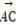 =sin2θ·
=sin2θ·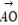 +cos2θ·
+cos2θ·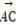 且sin2θ,
且sin2θ,
cos2θ∈[0,1],所以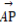 =(1-cos2θ)·
=(1-cos2θ)·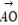 +cos2θ·
+cos2θ·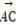 =
=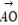 -cos2θ
-cos2θ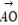 +cos2θ
+cos2θ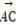 即
即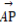 -
-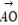 =cos2θ(
=cos2θ(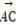 -
-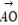 ),则
),则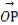 =cos2θ
=cos2θ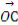 ,所以点P在线段OC上,故(
,所以点P在线段OC上,故(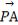 +
+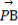 )·
)·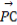 =2
=2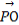 ·
·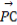 ,
,
设|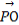 |=t(t∈[0,2]),
|=t(t∈[0,2]),
则(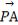 +
+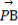 )·
)·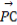 =2t(2-t)·(-1)=2t2-4t=2(t-1)2-2.
=2t(2-t)·(-1)=2t2-4t=2(t-1)2-2.
当t=1时取最小值-2.
【误区警示】本题容易因不能用向量的线性运算而得到向量共线的充要条件,即点P在线段OC上而导致解题错误或无法解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目