题目内容
△ABC中,角A,B,C所对的边分别为a,b,c,若a=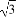 ,A=
,A= ,cosB=
,cosB=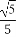 ,则b=( )
,则b=( )
(A) (B)
(B) (C)
(C) (D)
(D)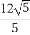
C
【解析】∵cosB= ,∴sinB=
,∴sinB=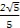 ,
,
∴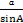 =
=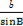 ,
,
则b=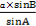 =
= =
=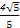 .
.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
△ABC中,角A,B,C所对的边分别为a,b,c,若a=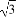 ,A=
,A= ,cosB=
,cosB=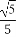 ,则b=( )
,则b=( )
(A) (B)
(B) (C)
(C) (D)
(D)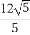
C
【解析】∵cosB= ,∴sinB=
,∴sinB=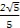 ,
,
∴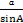 =
=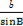 ,
,
则b=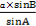 =
= =
=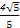 .
.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案